题目内容
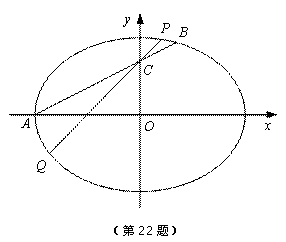
如图,点A(- a,0),B(![]() ,
,![]() )是椭圆
)是椭圆![]() 上的两点,直线AB与y轴交于点C(0,1).
上的两点,直线AB与y轴交于点C(0,1).
(1)求椭圆的方程;
(2)过点C任意作一条直线PQ与椭圆相交于P,Q,求PQ的取值范围.
 |
解:(1)由B(![]() ,
,![]() ),C(0,1),得直线BC方程为
),C(0,1),得直线BC方程为![]() .
.
令y = 0,得x = -2,∴a = 2.
将B(![]() ,
,![]() )代入椭圆方程,得
)代入椭圆方程,得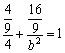 .∴b2 = 2.
.∴b2 = 2.
椭圆方程为![]() .
.
(2)① 当PQ与x轴垂直时,PQ = ![]() ;
;
② 当PQ与x轴不垂直时,不妨设直线PQ:y = kx + 1(k≥0),
代入椭圆方程x2 + 2y2 - 4 = 0,得x2 + 2(kx + 1)2 - 4 = 0.
即 (2k2 + 1) x2 + 4kx - 2 = 0.
设P(x1,y1),Q(x2,y2),则 ![]() .
.
则 | x1 - x2 | = ![]() .PQ =
.PQ = ![]() .
.
![]()
=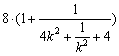 .
.
∵![]() ,在k =
,在k =![]() 时取等号,
时取等号,
∴PQ2 = 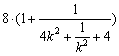 Î(8,9].则PQÎ
Î(8,9].则PQÎ![]() .
.
由①,②得PQ的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
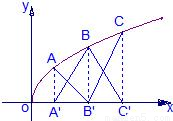
 如图,点A、B、C都在幂函数
如图,点A、B、C都在幂函数
 C
C 如图,点A、B、C都在幂函数
如图,点A、B、C都在幂函数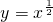 的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)
的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)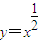 的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)
的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)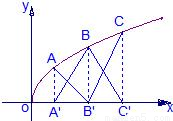
 的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)
的图象上,它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)