题目内容
设椭圆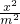 +
+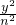 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的短轴长为
,则此椭圆的短轴长为
- A.

- B.

- C.

- D.

C
分析:先求出抛物线的焦点得到椭圆中的c=2,再根据离心率为 ,求出a=4,进而得到b的值即可得到结论.
,求出a=4,进而得到b的值即可得到结论.
解答:因为抛物线y2=8x的焦点为:(2,0),
由题得:椭圆的右焦点为(2,0),即c=2
又因为离心率为 ,
,
所以: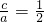 ?a=4,b=
?a=4,b= =2
=2
故2b=4 .
.
故选C.
点评:本题主要考查椭圆和抛物线的基本性质.注意求短轴长时,是2b不是b,避免错选B.
分析:先求出抛物线的焦点得到椭圆中的c=2,再根据离心率为
 ,求出a=4,进而得到b的值即可得到结论.
,求出a=4,进而得到b的值即可得到结论.解答:因为抛物线y2=8x的焦点为:(2,0),
由题得:椭圆的右焦点为(2,0),即c=2
又因为离心率为
 ,
,所以:
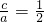 ?a=4,b=
?a=4,b= =2
=2
故2b=4
 .
.故选C.
点评:本题主要考查椭圆和抛物线的基本性质.注意求短轴长时,是2b不是b,避免错选B.

练习册系列答案
相关题目
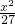 +
+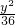 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程. +
+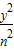 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,求椭圆的标准方程.
,求椭圆的标准方程.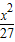 +
+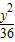 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.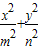 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的标准方程为 .
,则此椭圆的标准方程为 . +
+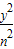 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的短轴长为( )
,则此椭圆的短轴长为( )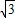
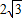

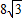
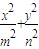 =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为 ,则此椭圆的标准方程为 .
,则此椭圆的标准方程为 .