ћвƒњƒЏ»Ё
“—÷™«ъѕяC£Їy=4x£ђCn£Їy=4x+n(n° N*)£ђі”C…ѕµƒµгQn£®xn£ђyn£©„чx÷бµƒієѕя£ђљїCn”ЏPn£ђ‘ўі”µгPn„чy÷бµƒієѕя£ђљїC”ЏµгQn+1£®xn+1£ђyn+1£©£ђ…иx1=1£ђan=xn+1-xn£ђbn=
£Ѓ
£®1£©«у эЅ–{xn}µƒЌ®ѕоєЂ љ£ї
£®2£©Љ«cn=
£ђ эЅ–{cn}µƒ«∞nѕоЇЌќ™Sn£ђ ‘±»љѕSn”л
µƒіу–°£®n° N*£©£ї
£®3£©Љ«dn=
£ђ эЅ–{dn}µƒ«∞nѕоЇЌќ™Tn£ђ ‘÷§√ч£Ї£®2n-1£©•dn°№T2n-1£Ѓ
| yn+1 |
| yn |
£®1£©«у эЅ–{xn}µƒЌ®ѕоєЂ љ£ї
£®2£©Љ«cn=
| 4 |
| anbn |
| 37 |
| 32 |
£®3£©Љ«dn=
| 3°Ѕ5n |
| 2n+2°Ѕ(bn-1) |
Ј÷ќц£Ї£®1£©“јћв“вµгPnµƒ„ш±кќ™£®xn£ђyn-1£©£ђі”ґшµ√µљyn+1=4xn+n=4xn+1£ђxn+1=xn+n£ђ”…іЋƒ№«у≥ц эЅ–{xn}µƒЌ®ѕоєЂ љ£Ѓ
£®2£©”…an=n£ђbn=4n£ђcn=
£ђ÷™S1=1£Љ
£ђS2=1+
=
£Љ
£ђS3=1+
+
=
£Љ
£ђµ±n£Њ3 ±£ђSn=
+
+
+°≠+
£Љ1+
+
+
+°≠+
£Љ
£Ѓ
£®3£©µ±n°Ё2£ђk=1£ђ2£ђ°≠£ђ2n-1 ±£ђ”–dk+d2n-k=
°Ѕ[
+
]°Ё
0£ђ”…іЋƒ№єїЌ∆µЉ≥цґ‘»ќ“вµƒn° N*£ђґЉ”–£®2n-1£©•dn°№T2n-1£Ѓ
£®2£©”…an=n£ђbn=4n£ђcn=
| 1 |
| n•4n-1 |
| 37 |
| 32 |
| 1 |
| 8 |
| 9 |
| 8 |
| 37 |
| 32 |
| 1 |
| 8 |
| 1 |
| 48 |
| 55 |
| 48 |
| 37 |
| 32 |
| 1 |
| 1 |
| 1 |
| 2°Ѕ4 |
| 1 |
| 3°Ѕ42 |
| 1 |
| n°Ѕ4n-1 |
| 1 |
| 2°Ѕ4 |
| 1 |
| 3°Ѕ42 |
| 1 |
| 3°Ѕ43 |
| 1 |
| 3°Ѕ4n-1 |
| 37 |
| 32 |
£®3£©µ±n°Ё2£ђk=1£ђ2£ђ°≠£ђ2n-1 ±£ђ”–dk+d2n-k=
| 3 |
| 4 |
| 5k |
| 2k°Ѕ(4k -1) |
| 52n-k |
| 22n-k°Ѕ(42n-k-1) |
| 6°Ѕ5n |
| 2n+2 |
|
љвір£Їљв£Ї£®1£©“јћв“вµгPnµƒ„ш±кќ™£®xn£ђyn-1£©£ђ
°аyn+1=4xn+n=4xn+1£ђ
°аxn+1=xn+n£ђ
°аxn=xn-1+n-1
=xn-2+£®n-2£©+£®n-1£©
=°≠=x1+1+2+°≠+£®n-1£©
=
+1£Ѓ
£®2£©”…£®1£©÷™£ђan=n£ђbn=4n£ђ
°яcn=
£ђ
°аS1=1£Љ
£ђS2=1+
=
£Љ
£ђ
S3=1+
+
=
£Љ
£ђ
°аµ±n£Њ3 ±£ђSn=
+
+
+°≠+
£Љ1+
+
+
+°≠+
=1+
+
°Ѕ
=
+
-
£Љ
£Ѓ
£®3£©µ±n°Ё2£ђk=1£ђ2£ђ°≠£ђ2n-1 ±£ђ”–£Ї
dk+d2n-k=
°Ѕ[
+
]
°Ё
°Ѕ2
=
=
£ђ
”÷°я4k+42n-k°Ё2°Ѕ4n£ђ
°а42n-4k-42n-k+1°№42n-2°Ѕ4n+1=£®4n-1£©2£ђ
°аdk+d2n-k°Ё
°Ѕ
=2dn£ђ
T2n-1°Ё
°Ѕ(2n-1)°Ѕ2dn=£®2n-1£©dn£ђ
°аґ‘»ќ“вµƒn° N*£ђґЉ”–£®2n-1£©•dn°№T2n-1£Ѓ
°аyn+1=4xn+n=4xn+1£ђ
°аxn+1=xn+n£ђ
°аxn=xn-1+n-1
=xn-2+£®n-2£©+£®n-1£©
=°≠=x1+1+2+°≠+£®n-1£©
=
| n(n-1) |
| 2 |
£®2£©”…£®1£©÷™£ђan=n£ђbn=4n£ђ
°яcn=
| 1 |
| n•4n-1 |
°аS1=1£Љ
| 37 |
| 32 |
| 1 |
| 8 |
| 9 |
| 8 |
| 37 |
| 32 |
S3=1+
| 1 |
| 8 |
| 1 |
| 48 |
| 55 |
| 48 |
| 37 |
| 32 |
°аµ±n£Њ3 ±£ђSn=
| 1 |
| 1 |
| 1 |
| 2°Ѕ4 |
| 1 |
| 3°Ѕ42 |
| 1 |
| n°Ѕ4n-1 |
£Љ1+
| 1 |
| 2°Ѕ4 |
| 1 |
| 3°Ѕ42 |
| 1 |
| 3°Ѕ43 |
| 1 |
| 3°Ѕ4n-1 |
=1+
| 1 |
| 8 |
| 1 |
| 3 |
| ||||
1-
|
=
| 9 |
| 8 |
| 1 |
| 36 |
| 1 |
| 9°Ѕ4n-1 |
| 37 |
| 32 |
£®3£©µ±n°Ё2£ђk=1£ђ2£ђ°≠£ђ2n-1 ±£ђ”–£Ї
dk+d2n-k=
| 3 |
| 4 |
| 5k |
| 2k°Ѕ(4k -1) |
| 52n-k |
| 22n-k°Ѕ(42n-k-1) |
°Ё
| 3 |
| 4 |
|
=
| 3°Ѕ2°Ѕ5n |
| 4°Ѕ2n |
|
=
| 6°Ѕ5n |
| 2n+2 |
|
”÷°я4k+42n-k°Ё2°Ѕ4n£ђ
°а42n-4k-42n-k+1°№42n-2°Ѕ4n+1=£®4n-1£©2£ђ
°аdk+d2n-k°Ё
| 6°Ѕ5n |
| 2n+2 |
| 1 |
| 4n-1 |
T2n-1°Ё
| 1 |
| 2 |
°аґ‘»ќ“вµƒn° N*£ђґЉ”–£®2n-1£©•dn°№T2n-1£Ѓ
µг∆ј£Ї±ЊћвњЉ≤й эЅ–µƒЌ®ѕоєЂ љµƒ«уЈ®£ђњЉ≤йЅљЄц эіу–°µƒ±»љѕ£ђњЉ≤й≤їµ» љµƒ÷§√ч£ђљвћв ±“™»ѕ’ж…ућв£ђ„Ґ“вµ»Љџ„™їѓЋЉѕлµƒЇѕјн‘Ћ”√£Ѓ

ЅЈѕ∞≤бѕµЅ–ір∞Є
 ±Є’љ÷–њЉЇЃЉўѕµЅ–ір∞Є
±Є’љ÷–њЉЇЃЉўѕµЅ–ір∞Є
ѕаєЎћвƒњ
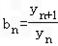 £Ѓ
£Ѓ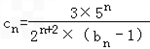 £ђ эЅ–{cn}µƒ«∞nѕоЇЌќ™Tn£ђ
£ђ эЅ–{cn}µƒ«∞nѕоЇЌќ™Tn£ђ £ї
£ї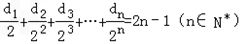 £ђЉ« эЅ–{an}µƒ«∞nѕоЇЌќ™An£ђ эЅ–{dn}µƒ«∞nѕоЇЌќ™Bn£ђ ‘±»љѕAn”л
£ђЉ« эЅ–{an}µƒ«∞nѕоЇЌќ™An£ђ эЅ–{dn}µƒ«∞nѕоЇЌќ™Bn£ђ ‘±»љѕAn”л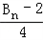 µƒіу–°£Ѓ
µƒіу–°£Ѓ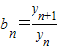 £Ѓ
£Ѓ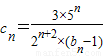 £ђ эЅ–{cn}µƒ«∞nѕоЇЌќ™Tn£ђ«у÷§£Ї
£ђ эЅ–{cn}µƒ«∞nѕоЇЌќ™Tn£ђ«у÷§£Ї £ї
£ї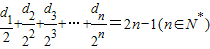 £ђЉ« эЅ–{an}µƒ«∞nѕоЇЌќ™An£ђ эЅ–{dn}µƒ«∞nѕоЇЌќ™Bn£ђ ‘±»љѕAn”л
£ђЉ« эЅ–{an}µƒ«∞nѕоЇЌќ™An£ђ эЅ–{dn}µƒ«∞nѕоЇЌќ™Bn£ђ ‘±»љѕAn”л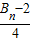 µƒіу–°£Ѓ
µƒіу–°£Ѓ