题目内容
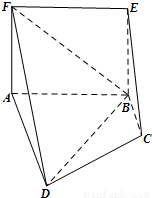
 如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
(Ⅰ)证明:C,D,F,E四点共面;
(Ⅱ)设AB=BC=BE,求二面角A-ED-B的大小.
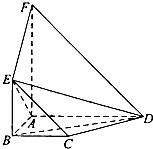
分析:(Ⅰ)延长DC交AB的延长线于点G,延长FE交AB的延长线于G′,根据比例关系可证得G与G′重合,准确推理,得到直线CD、EF相交于点G,即C,D,F,E四点共面.
(Ⅱ)取AE中点M,作MN⊥DE,垂足为N,连接BN,由三垂线定理知BN⊥ED,根据二面角平面角的定义可知∠BMN为二面角A-ED-B的平面角,在三角形BMN中求出此角即可.
(Ⅱ)取AE中点M,作MN⊥DE,垂足为N,连接BN,由三垂线定理知BN⊥ED,根据二面角平面角的定义可知∠BMN为二面角A-ED-B的平面角,在三角形BMN中求出此角即可.
解答:解:(Ⅰ)延长DC交AB的延长线于点G,由BC
AD得
=
=
=
延长FE交AB的延长线于G′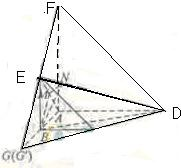
同理可得
=
=
=
故
=
,即G与G′重合
因此直线CD、EF相交于点G,即C,D,F,E四点共面.
(Ⅱ)设AB=1,则BC=BE=1,AD=2
取AE中点M,则BM⊥AE,又由已知得,AD⊥平面ABEF
故AD⊥BM,BM与平面ADE内两相交直线AD、AE都垂直.
所以BM⊥平面ADE,作MN⊥DE,垂足为N,连接BN
由三垂线定理知BN⊥ED,∠BMN为二面角A-ED-B的平面角.BM=
,MN=
•
=
故tan∠BMN=
=
所以二面角A-ED-B的大小arctan
| ∥ |
. |
| 1 |
| 2 |
| GB |
| GA |
| GC |
| GD |
| BC |
| AD |
| 1 |
| 2 |
延长FE交AB的延长线于G′

同理可得
| G′E |
| G′F |
| G′B |
| G′A |
| BE |
| AF |
| 1 |
| 2 |
故
| G′B |
| G′A |
| GB |
| GA |
因此直线CD、EF相交于点G,即C,D,F,E四点共面.
(Ⅱ)设AB=1,则BC=BE=1,AD=2
取AE中点M,则BM⊥AE,又由已知得,AD⊥平面ABEF
故AD⊥BM,BM与平面ADE内两相交直线AD、AE都垂直.
所以BM⊥平面ADE,作MN⊥DE,垂足为N,连接BN
由三垂线定理知BN⊥ED,∠BMN为二面角A-ED-B的平面角.BM=
| ||
| 2 |
| 1 |
| 2 |
| AD×AE |
| DE |
| ||
| 3 |
故tan∠BMN=
| BM |
| MN |
| ||
| 2 |
所以二面角A-ED-B的大小arctan
| ||
| 2 |
点评:此题重点考查立体几何中四点共面问题和求二面角的问题,考查空间想象能力,几何逻辑推理能力,以及计算能力;突破:熟悉几何公理化体系,准确推理,注意书写格式是顺利进行求解的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC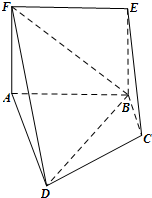 如图,四边形ABCD为直角梯形,AD∥BC,AD⊥CD.AD=AB=2BC,四边形ABEF为矩形,平面ABEF⊥平面ABCD.
如图,四边形ABCD为直角梯形,AD∥BC,AD⊥CD.AD=AB=2BC,四边形ABEF为矩形,平面ABEF⊥平面ABCD. 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.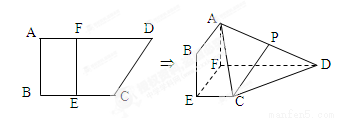
 ,求实数k的值.
,求实数k的值.