题目内容
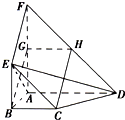
 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥ = |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
(1)求证:C、D、F、E四点共面;
(2)设AB=BE,求证:平面ADE⊥平面DCE;
(3)设AB=BC=BE,求二面角A-ED-B的余弦值.
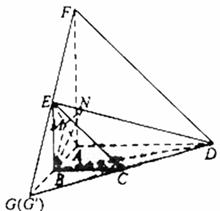
分析:(1)以A为坐标原点,射线AB为x轴正半轴,建立如图的直角坐标系A-xyz,设AB=a,BC=b,BE=c,通过向量法可证得EC∥FD,即C、D、E、F共面
(2)求出平面ADE的法向量和平面DCE的法向量,利用向量垂直的充要条件可得两个法向量垂直,进而平面ADE⊥平面DCE;
(3)求出平面ADE的法向量为
=(1,0,-1),和平面BDE的法向量,代入向量夹角公式可得二面角A-ED-B的余弦值
(2)求出平面ADE的法向量和平面DCE的法向量,利用向量垂直的充要条件可得两个法向量垂直,进而平面ADE⊥平面DCE;
(3)求出平面ADE的法向量为
| m |
解答:解:由平面平面ABEF⊥平面ABCD,AF⊥AB,得AF⊥平面ABCD,以A为坐标原点,射线AB为x轴正半轴,建立如图的直角坐标系A-xyz,…(1分)

证明:(1)设AB=a,BC=b,BE=c,
则B(a,0,0),C(a,b,0),E(a,0,c),D(0,2b,0),F(0,0,2c),…(3分)
∴
=(0,b,-c),
=(0,2b,-2c),
故
=
,
∴EC∥FD,
∴C、D、E、F共面.…(5分)
解:(2)∵AB=BE,由(1)可知E(a,0,a),
∴
=(a,0,a),
=(0,2b,0),
设
=(x,y,z)为平面ADE的法向量,则
,∴
=(1,0,-1),…(7分)
设
=(x,y,z)为平面DCE的法向量,则由
=(0,b,-a),
=(-a,b,0),
∴
,∴
=(1.
,1),…(9分)
∵
•
=0,
∴
⊥
,
∴平面ADE⊥平面DCE;
(3)当AB=BC=BE时,由(2)可知平面ADE的法向量为
=(1,0,-1),
设平面BDE的法向量为
=(x,y,z),
由
=(0,0,a),
=(-a,2a,0)得
,
∴
=(2,1,0),
∴cos<
,
>=
=
=
,
∴二面角A-ED-B的余弦值为
.…(16分)

证明:(1)设AB=a,BC=b,BE=c,
则B(a,0,0),C(a,b,0),E(a,0,c),D(0,2b,0),F(0,0,2c),…(3分)
∴
| EC |
| FD |
故
| EC |
| 1 |
| 2 |
| FD |
∴EC∥FD,
∴C、D、E、F共面.…(5分)
解:(2)∵AB=BE,由(1)可知E(a,0,a),
∴
| AE |
| AD |
设
| m |
|
| m |
设
| n |
| EC |
| CD |
∴
|
| n |
| a |
| b |
∵
| m |
| n |
∴
| m |
| n |
∴平面ADE⊥平面DCE;
(3)当AB=BC=BE时,由(2)可知平面ADE的法向量为
| m |
设平面BDE的法向量为
| u |
由
| BE |
| BD |
|
∴
| u |
∴cos<
| m |
| u |
| ||||
|
|
| 2 | ||||
|
| ||
| 5 |
∴二面角A-ED-B的余弦值为
| ||
| 5 |
点评:本题考查的知识点是有空间向量求平面间的夹角,建立空间坐标系将空间线线垂直及二面角转化为向量垂直及向量夹角问题是解答的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
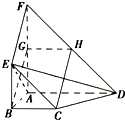 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC