题目内容
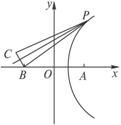
A、B、C是我方三个炮兵阵地，A在B正东6 km，C在B正北偏西30°，相距4 km，P为敌炮阵地，某时刻A处发现敌炮阵地的某种信号，由于B、C两地比A距P地远，因此4 s后，B、C才同时发现这一信号，此信号的传播速度为1 km/s，A若炮击P地，求炮击的方位角．分析：建立坐标系，因为|PB|=|PC|，所以点P在线段BC的垂直平分线上，写出中垂线的方程，又|PB|-|PA|=4，故P在以A、B为焦点的双曲线右支上，写出双曲线方程，将这2个方程联立方程组，解出交点P的坐标，由PA斜率计算炮击的方位角．
解答：
解：如图，以直线BA为x轴，线段BA的中垂线为y轴建立坐标系，则
B（-3，0）、A（3，0）、C（-5，2
）．
因为|PB|=|PC|，所以点P在线段BC的垂直平分线上．
因为kBC=-
，BC中点D（-4，
），
所以直线PD的方程为y-
=
（x+4）．①
又|PB|-|PA|=4，故P在以A、B为焦点的双曲线右支上．
设P（x，y），则双曲线方程为
-
=1（x≥0）．②
联立①②，得x=8，y=5
，
所以P（8，5
）．因此kPA=
=
．
故炮击的方位角为北偏东30°．
解：如图，以直线BA为x轴，线段BA的中垂线为y轴建立坐标系，则B（-3，0）、A（3，0）、C（-5，2
| 3 |
因为|PB|=|PC|，所以点P在线段BC的垂直平分线上．
因为kBC=-
| 3 |
| 3 |
所以直线PD的方程为y-
| 3 |
| 1 | ||
|
又|PB|-|PA|=4，故P在以A、B为焦点的双曲线右支上．
设P（x，y），则双曲线方程为
| x2 |
| 4 |
| y2 |
| 5 |
联立①②，得x=8，y=5
| 3 |
所以P（8，5
| 3 |
5
| ||
| 8-3 |
| 3 |
故炮击的方位角为北偏东30°．
点评：本题考查双曲线方程的应用．
练习册系列答案
相关题目
