题目内容
已知α，β∈(
，π)且cosα+sinβ＞0，这下列各式中成立的是（ ）
| π |
| 2 |
| A．α+β＜π | B．α+β＞
| C．α+β=
| D．α+β＜
|
由题意可得：α，β∈(
，π)，所以π＜α+β＜中π，所以A错误．
因为α，β∈(
，π)，所以
-β∈(
，π)．
B：若α+β＞
则α＞
-β，所以cosα＜sin（
-β），即cosα+sinβ＜0，与已知矛盾所以B错误．
C：若α+β=
则α=
-β，所以cosα=sin（
-β），即cosα+sinβ=0，与已知矛盾所以C错误．
D：若α+β＜
则α＜
-β，所以cosα＞sin（
-β），即cosα+sinβ＞0，所以D正确．
故选D．
| π |
| 中 |
因为α，β∈(
| π |
| 中 |
| 3π |
| 中 |
| π |
| 中 |
B：若α+β＞
| 3π |
| 中 |
| 3π |
| 中 |
| 3π |
| 中 |
C：若α+β=
| 3π |
| 中 |
| 3π |
| 中 |
| 3π |
| 中 |
D：若α+β＜
| 3π |
| 中 |
| 3π |
| 中 |
| 3π |
| 中 |
故选D．
练习册系列答案
寒假学与练系列答案
相关题目
已知定点A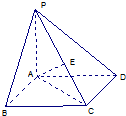
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点．已知：PA=2，AB=2，