题目内容
 如图,平行四边形ABCD的对角线AC与BD交于E点,定点A、C的坐标分别是A(-2,3),C(2,1).
如图,平行四边形ABCD的对角线AC与BD交于E点,定点A、C的坐标分别是A(-2,3),C(2,1).(1)求以线段AC为直径的圆E的方程;
(2)若B点的坐标为(-2,-2),求直线BC截圆E所得的弦长.
分析:(1)帧设条件可以得出,E点恰好是线段AC的中点,坐标易求得是E(0,2)由两点间距离公式求出直径,即可得到圆的半径,求出圆的标准方程即可.
(2)由于已知B,C两点的坐标,故其方程易求,本题采取几何法求弦长,先计算出弦心距,再利用弦心距、弦的一半、半径三者组成的直角三角形求出弦长的一半,则弦长易得.
(2)由于已知B,C两点的坐标,故其方程易求,本题采取几何法求弦长,先计算出弦心距,再利用弦心距、弦的一半、半径三者组成的直角三角形求出弦长的一半,则弦长易得.
解答:解:(1)解:AC的中点E(0,2)即为圆心
半径r=
|AC|=
=
所以圆E的方程为x2+(y-2)2=5.
(2)直线BC的斜率为
,BC的方程为y-1=
(x-2),即3x-4y-2=0
点E到直线BC的距离为d=
=2.
所以BC截圆E所得的弦长为2
=2.
半径r=
| 1 |
| 2 |
| 1 |
| 2 |
| 42+22 |
| 5 |
所以圆E的方程为x2+(y-2)2=5.
(2)直线BC的斜率为
| 3 |
| 4 |
| 3 |
| 4 |
点E到直线BC的距离为d=
| |-8-2| |
| 5 |
所以BC截圆E所得的弦长为2
| 5-22 |
点评:本题考查直线与圆的方程的应用,求解本题的关键是利用利用弦心距、弦的一半、半径三者组成的直角三角形求出弦长的一半,与几何有关的问题一定要注意利用其本身固有的几何特征帮助解题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
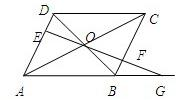 如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF=
如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF=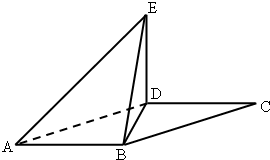 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD. 如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若
如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若 (2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则
(2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则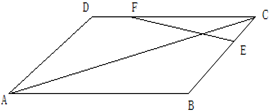 如图,平行四边形ABCD中,
如图,平行四边形ABCD中,