Question

【题目】已知函数f（x）=（ ）x ， 其反函数为y=g（x）．
（1）若g（mx2+2x+1）的定义域为R，求实数m的取值范围；
（2）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值h（a）；
（3）是否存在实数m＞n＞3，使得函数y=h（x）的定义域为[n，m]，值域为[n2 ， m2]，若存在，求出m、n的值；若不存在，则说明理由．

Answer 1

【答案】
（1）解：∵函数f（x）=（ ）x，则其反函数为y=g（x）= =﹣log3x．

∴g（mx2+2x+1）=﹣ ，

当m≤0时，g（mx2+2x+1）的定义域不为R，舍去．

当m＞0时，g（mx2+2x+1）的定义域为R，则 ，解得m＞1．

∴实数m的取值范围是（1，+∞）

（2）解：函数y=[f（x）]2﹣2af（x）+3= ﹣2a +3，

∵x∈[﹣1，1]时，令 =t∈ ，

∴y=t2﹣2at+3=（t﹣a）2+3﹣a2=u（t），对称轴t=a．

当a 时，u（t）在t∈ 上单调递增，∴t= 时，u（t）取得最小值u（ ）= ．

当a≥3时，u（t）在t∈ 上单调递减，∴t=3时，u（t）取得最小值u（3）=12﹣6a．

当 ＜a＜3时，u（t）在t∈ 上单调递减，在t∈[a，3]上单调递增，∴t=a时，u（t）取得最小值u（a）=3﹣a2．

综上可得：最小值h（a）=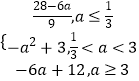

（3）解：存在实数m＞n＞3，使得函数y=h（x）=﹣6x+12的定义域为[n，m]，值域为[n2，m2]，

则 ，可得：m2﹣6m+24=0，由于△=36﹣96＜0，因此上述方程无解．

于是假设不成立，

因此不存在实数m＞n＞3，使得函数y=h（x）=﹣6x+12的定义域为[n，m]，值域为[n2，m2]．

【解析】（1）函数f（x）=（ ）x ， 则其反函数为y=g（x）= ．可得g（mx2+2x+1）=﹣ ，当m≤0时，舍去．当m＞0时，g（mx2+2x+1）的定义域为R，可得 ，解得m即可得出．（2）函数y=[f（x）]2﹣2af（x）+3= ﹣2a +3，x∈[﹣1，1]时，令 =t∈ ，y=（t﹣a）2+3﹣a2=u（t），对称轴t=a．对a与 ，3的大小分类讨论，利用二次函数的单调性即可得出．（3）存在实数m＞n＞3，使得函数y=h（x）=﹣6x+12的定义域为[n，m]，值域为[n2 ， m2]，可得 ，解出即可判断出结论．