题目内容
设f(x)=sin(x-sinx),x∈R.关于f(x)有以下结论:①f(x)是奇函数;
②f(x)的值域是[0,1];
③f(x)是周期函数;
④x=π是函数y=f(x)图象的一条对称轴;
⑤f(x)在[0,π]上是增函数.
其中正确结论的序号是 .
【答案】分析:根据已知求出f(-x)的解析式,并分析它是否与f(x)相等,结合函数奇偶性的定义可判断①的真假,
根据内函数的值域为R,结合正弦函数的性质可判断②的真假;
求出f(x+2π)的解析式,并分析它是否与f(x)相等,结合函数周期性的定义可判断③的真假,
求出f(π+x)与f(π-x)的解析式,并分析它们是否相等,结合函数对称性的定义可判断④的真假,
求出函数的导函数,分析导函数的符号,可判断⑤的真假.
解答:解:∵f(x)=sin(x-sinx),
∴f(-x)=sin[-x-sin(-x)]=sin(-x+sinx)=sin[-(x-sinx)]=-sin(x-sinx)=-f(x),故函数f(x)是奇函数,即①正确;
令u=x-sinx,则u∈R,则f(x)∈[-1,1],即f(x)的值域是[-1,1],即②错误;
f(x+2π)=sin[x+2π-sin(x+2π)]=sin(x+2π-sinx)=sin(x-sinx)=f(x),故f(x)是周期函数,即③正确;
∵f(π+x)=sin[π+x-sin(π+x)]=sin(π+x+sinx)=-sin(x+sinx);f(π-x)=sin[π-x-sin(π-x)]=sin(π-x-sinx)=sin(x+sinx),故(π,0)是y=f(x)图象的一个对称中心,故④错误;
∵f′(x)=cos(x-sinx)(1-cosx),当x∈(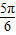 ,π)时,f′(x)<0,函数为减函数,故⑤错误;
,π)时,f′(x)<0,函数为减函数,故⑤错误;
故答案为:①③
点评:本题以命题的真假判断为载体考查了三角函数的奇偶性,值域,周期性,对称性,单调性,复合函数等,是函数图象和性质的综合应用,难度较大.
根据内函数的值域为R,结合正弦函数的性质可判断②的真假;
求出f(x+2π)的解析式,并分析它是否与f(x)相等,结合函数周期性的定义可判断③的真假,
求出f(π+x)与f(π-x)的解析式,并分析它们是否相等,结合函数对称性的定义可判断④的真假,
求出函数的导函数,分析导函数的符号,可判断⑤的真假.
解答:解:∵f(x)=sin(x-sinx),
∴f(-x)=sin[-x-sin(-x)]=sin(-x+sinx)=sin[-(x-sinx)]=-sin(x-sinx)=-f(x),故函数f(x)是奇函数,即①正确;
令u=x-sinx,则u∈R,则f(x)∈[-1,1],即f(x)的值域是[-1,1],即②错误;
f(x+2π)=sin[x+2π-sin(x+2π)]=sin(x+2π-sinx)=sin(x-sinx)=f(x),故f(x)是周期函数,即③正确;
∵f(π+x)=sin[π+x-sin(π+x)]=sin(π+x+sinx)=-sin(x+sinx);f(π-x)=sin[π-x-sin(π-x)]=sin(π-x-sinx)=sin(x+sinx),故(π,0)是y=f(x)图象的一个对称中心,故④错误;
∵f′(x)=cos(x-sinx)(1-cosx),当x∈(
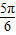 ,π)时,f′(x)<0,函数为减函数,故⑤错误;
,π)时,f′(x)<0,函数为减函数,故⑤错误;故答案为:①③
点评:本题以命题的真假判断为载体考查了三角函数的奇偶性,值域,周期性,对称性,单调性,复合函数等,是函数图象和性质的综合应用,难度较大.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
下列命题中正确的是( )
A、设f(x)=sin(2x+
| ||||||
B、?x0∈R.便得
| ||||||
C、设f(x)=cos(x+
| ||||||
D、设f(x)=2sin2x,则f(x+
|