题目内容
化简
（1）lg25+lg2×lg50+（lg2）2
（2）当8＜x＜10时，化简
+
．
（1）lg25+lg2×lg50+（lg2）2
（2）当8＜x＜10时，化简
| (x-8)2 |
| (x-10)2 |
考点：对数的运算性质
专题：函数的性质及应用
分析：（1）利用对数的性质和运算法则求解．
（2）利用绝对值的性质和根式的运算法则求解．
（2）利用绝对值的性质和根式的运算法则求解．
解答：
解：（1）lg25+lg2×lg50+（lg2）2
=2lg5+lg2（lg2+2lg5）+（lg2）2
=2lg5+2（lg2）2+2lg2lg5
=2lg5+2lg2（lg2+lg5）
=2lg5+2lg2
=2．
（2）∵8＜x＜10，
∴
+
=（x-8）+（10-x）=2．
=2lg5+lg2（lg2+2lg5）+（lg2）2
=2lg5+2（lg2）2+2lg2lg5
=2lg5+2lg2（lg2+lg5）
=2lg5+2lg2
=2．
（2）∵8＜x＜10，
∴
| (x-8)2 |
| (x-10)2 |
点评：本题考查对数式和根式的化简求值，是基础题，解题时要注意对数的性质和运算法则、绝对值的性质和根式的运算法则的合理运用．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
下列四组中的函数f（x）与g（x），是同一函数的是（ ）
| A、f（x）=ln（1-x）+ln（1+x），g（x）=ln（1-x2） | ||||||
| B、f（x）=lgx2，g（x）=2lgx | ||||||
C、f（x）=
| ||||||
D、f（x）=
|
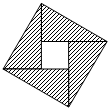三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（ ）”的几何解释．| A、如果a＞b，b＞c，那么a＞c |
| B、如果a＞b＞0，那么a2＞b2 |
| C、对任意实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立 |
| D、如果a＞b，c＞0那么ac＞bc |
在（x+y）n的展开式中，若第8项系数最大，则n的值可能等于（ ）
| A、14，15 |
| B、15，16 |
| C、16，17 |
| D、14，15，16 |
命题“?x0∈R，使得x03＜0”的否定为（ ）
| A、?x0∈R，使得x03≥0 |
| B、?x∈R，x3＜0 |
| C、?x∈R，使得x3≤0 |
| D、?x∈R，x3≥0 |