题目内容
已知圆C:
，过定点P(0 , 1)作斜率为1的直线交圆C于A、B两点，P为线段AB的中点.
（Ⅰ）求
的值；
（Ⅱ）设E为圆C上异于A、B的一点，求△ABE面积的最大值；
（Ⅲ）从圆外一点M向圆C引一条切线，切点为N，且有|MN|=|MP| , 求|MN|的最小值，并求|MN|取最小值时点M的坐标.
（Ⅰ） 
（Ⅱ）
（Ⅲ）
|MN|的最小值
M点坐标为
解析:
（Ⅰ）由题知圆心C(
)，又P（0，1）为线段AB的中点，
,即
（Ⅱ）由（Ⅰ）知圆C的方程为
圆心C(-1, 2),半径R=2，
又直线AB的方程是
圆心C到AB得距离
当
时，△ABE面积最大，
（Ⅲ） 
切线MN
CN, 
, 又 |MN|=|MP|, 
设M(
)，则有
，化简得：
即点M在上，|MN|的最小值即为|MP|的最小值
，解方程组：
得：
满足条件的M点坐标为
练习册系列答案
相关题目
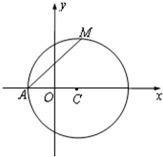已知圆C：（x-1）2+y2=r2（r＞1），设A为圆C与x轴负半轴的交点，过点A作圆C的弦AM，并使弦AM的中点恰好落在y轴上．
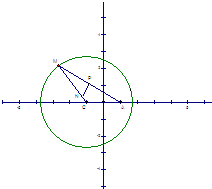如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆C上一动点，点P在线段AM上，点N在线段CM上，且满足
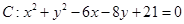，直线
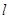过定点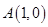
.
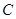的坐标和圆的半径
；
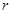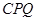面积的最大值，并求此时
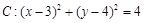，直线
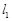过定点
A (1，0)．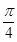
，