Question

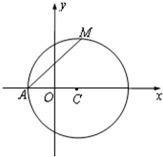已知圆C：（x-1）²+y²=r²（r＞1），设A为圆C与x轴负半轴的交点，过点A作圆C的弦AM，并使弦AM的中点恰好落在y轴上．
（1）当r在（1，+∞）内变化时，求点M的轨迹E的方程；
（2）设轨迹E的准线为l，N为l上的一个动点，过点N作轨迹E的两条切线，切点分别为P，Q．求证：直线PQ必经过x轴上的一个定点B，并写出点B的坐标．

Answer 1

分析：（1）设M（x，y），则AM的中点D(0，

y

2

)．因为C（1，0），

DC

=(1，-

y

2

)，

DM

=(x，

y

2

)．在⊙C中，因为CD⊥DM，所以，

DC

•

DM

=0，由此能求出点M的轨迹E的方程．
（2）轨迹E的准线l：x=-1，所以，可设N（-1，t），过N的斜率存在的直线方程为：y-t=k（x+1），由

y2=4x y=kx+(k+t)

得

k

4

y2-y+(k+t)=0．由△=1-k（k+t）=0得：k²+kt-1=0．由此入手能够证明直线PQ必经过x轴上的一个定点B，并能求出B的坐标．

解答：解：（1）设M（x，y），则AM的中点D(0，

y

2

)．
因为C（1，0），

DC

=(1，-

y

2

)，

DM

=(x，

y

2

)．
在⊙C中，因为CD⊥DM，所以，

DC

•

DM

=0，
所以x-

y2

4

=0．
所以，y²=4x（x≠0）
所以，点M的轨迹E的方程为：y²=4x（x≠0）（5分）（说明漏了x≠0不扣分）
（2）轨迹E的准线l：x=-1
所以，可设N（-1，t），过N的斜率存在的直线方程为：y-t=k（x+1）
由

y2=4x y=kx+(k+t)

得

k

4

y2-y+(k+t)=0．
由△=1-k（k+t）=0得：k²+kt-1=0．
设直线NP，NQ斜率分别为k₁，k₂，则k₁k₂=-1①且yp=

2

k1

，yQ=

2

k2

所以P(

2

k12

，

2

k1

)，Q(

2

k22

，

2

k2

)
所以，直线PQ的方程：(y-

2

k1

)(k1+k2)=2k1k2(x-

2

k12

)．
令y=0，则x=

1

k12

-

k1+k2

k12k2

=

-k1

k12k2

=-

-1

k1k2

由①知，x=1即直线PQ过定点B（1，0）．（10分）

点评：本题考查直线和圆锥曲线的位置关系的综合运用，解题时要认真审题，注意挖掘题设中的隐含条件．