题目内容
16.已知复数z满足z•(i-1)=1+i,则z的共轭复数$\overline{z}$的虚部是( )| A. | 1 | B. | -i | C. | i | D. | -1 |
分析 把已知等式变形,然后复数代数形式的乘除运算化简复数z,求出$\overline{z}$,则答案可求.
解答 解:由z•(i-1)=1+i,
得$z=\frac{1+i}{-1+i}=\frac{(1+i)(-1-i)}{(-1+i)(-1-i)}$=$\frac{-2i}{2}=-i$.
则z的共轭复数$\overline{z}$=i,虚部是:1.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4.在△ABC中,AC=2AB=2,∠BAC=120°,O是BC的中点,M是AO上一点,且$\overrightarrow{AO}$=3$\overrightarrow{MO}$,则$\overrightarrow{MB}$$•\overrightarrow{MC}$的值是( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{7}{6}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{6}$ |
11.执行如图所示的程序框图,若输入的a,b分别为36,28,则输出的a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 20 |
1.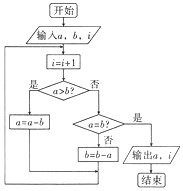 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )| A. | 2,5 | B. | 2,4 | C. | 0,4 | D. | 0,5 |
8.已知i为虚数单位,则$\frac{1+i}{3-i}$=( )
| A. | $\frac{2-i}{5}$ | B. | $\frac{2+i}{5}$ | C. | $\frac{1-2i}{5}$ | D. | $\frac{1+2i}{5}$ |
20.若复数z满足$\frac{3+4i}{i}$=$\frac{z}{1+i}$,则z等于( )
| A. | 7+i | B. | 7-i | C. | 7+7i | D. | -7+7i |