题目内容
如图,点P是正方形ABCD外一点,PA 平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.
平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.
(1)求证:EF//平面PAD;
(2)求证:EF 平面PCD;
平面PCD;
(3)求:直线BD与平面EFC所成角的大小.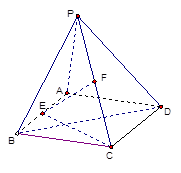
 平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.
平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.(1)求证:EF//平面PAD;
(2)求证:EF
 平面PCD;
平面PCD;(3)求:直线BD与平面EFC所成角的大小.

(1)取PD中点M,连结AM,FM
由FM//CD,FM= CD,得FM//AE,FM=AE,
CD,得FM//AE,FM=AE, 四边形AEFM是平行四边形
四边形AEFM是平行四边形
 EF//AM,又AM
EF//AM,又AM 面PAD,
面PAD, EF//面PAD
EF//面PAD
(2) PA
PA 面ABCD
面ABCD  PA
PA CD,又AD
CD,又AD CD
CD  CD
CD 面PAD
面PAD  AM
AM CD
CD
又 PA="AB=2"
PA="AB=2"  AM
AM PD
PD  AM
AM 面PCD
面PCD  EF
EF 面PCD
面PCD
(3)过点D作DN PC交于点N,设BD与EC交于点Q,连结QN
PC交于点N,设BD与EC交于点Q,连结QN
由(2)知 DQN为所求角
DQN为所求角  DN=
DN= ,DQ=
,DQ=
 Rt
Rt DNQ中,sin
DNQ中,sin  DQN=
DQN= =
=

 DQN=
DQN=
由FM//CD,FM=
 CD,得FM//AE,FM=AE,
CD,得FM//AE,FM=AE, 四边形AEFM是平行四边形
四边形AEFM是平行四边形 EF//AM,又AM
EF//AM,又AM 面PAD,
面PAD, EF//面PAD
EF//面PAD(2)
 PA
PA 面ABCD
面ABCD  PA
PA CD,又AD
CD,又AD CD
CD  CD
CD 面PAD
面PAD  AM
AM CD
CD又
 PA="AB=2"
PA="AB=2"  AM
AM PD
PD  AM
AM 面PCD
面PCD  EF
EF 面PCD
面PCD(3)过点D作DN
 PC交于点N,设BD与EC交于点Q,连结QN
PC交于点N,设BD与EC交于点Q,连结QN由(2)知
 DQN为所求角
DQN为所求角  DN=
DN= ,DQ=
,DQ=
 Rt
Rt DNQ中,sin
DNQ中,sin  DQN=
DQN= =
=

 DQN=
DQN=
略

练习册系列答案
相关题目
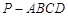 中,底面
中,底面 为矩形,
为矩形,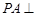 平面
平面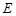 在线段
在线段 上,
上,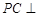 平面
平面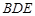 .
.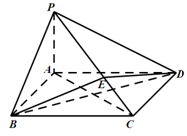
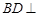 平面
平面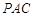 ;
;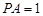 ,
,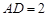 ,求二面角
,求二面角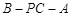 的正切值.
的正切值.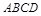 中,
中,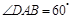 .点
.点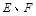 分别在边
分别在边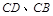 上,点
上,点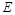 与点
与点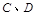 不重合,
不重合,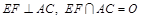 .沿
.沿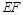 将
将 翻折到
翻折到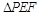 的位置,使平面
的位置,使平面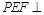 平面
平面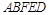 .
.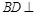 平面
平面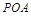 ;
;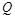 满足
满足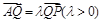 ,试探究:当
,试探究:当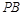 取得最小值时,直线
取得最小值时,直线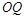 与平面
与平面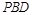 所成角的大小是否一定大于
所成角的大小是否一定大于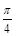 ?并说明理由.
?并说明理由.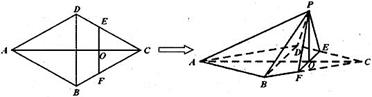
 ,M是棱
,M是棱 的中点,N是棱
的中点,N是棱 的中点.
的中点. 所成角的正弦值;
所成角的正弦值; 的体积.
的体积.
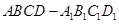 中,
中,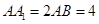 ,点
,点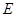 在
在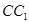 上且
上且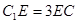 .
.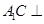 平面
平面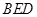 ;
;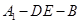 的余弦值大小.
的余弦值大小.
 并确定
并确定 的关系,使
的关系,使 轴垂直.
轴垂直. ABC的重心,则
ABC的重心,则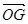 等于
等于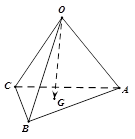


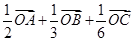
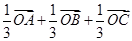
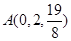 ,
,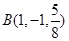 ,
,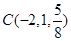 是平面
是平面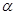 内的三点,设平面
内的三点,设平面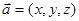 ,则
,则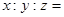 ______________
______________