题目内容
11.对于函数f(x)=$\frac{x}{1+|x|}$,给出下列结论:①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(-1,1)
③函数g(x)=f(x)-x在R上有三个零点;
④若x1≠x2,则$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0
⑤若x1<x2,则$\frac{f({x}_{1})+f({x}_{2})}{2}$$<f(\frac{{x}_{1}+{x}_{2}}{2})$
其中所有正确结论的序号为①②④.
分析 f(x)=$\frac{x}{1+|x|}$,f(-x)=$\frac{-x}{1+|x|}$;从而可得f(-x)+f(x)=0在x∈R时恒成立;f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$,从而可求得-1<f(x)<1;g(x)=f(x)-x=$\left\{\begin{array}{l}{\frac{-{x}^{2}}{1+x},x≥0}\\{\frac{{x}^{2}}{1-x},x<0}\end{array}\right.$,从而可知函数g(x)=f(x)-x在R上有一个零点;化简f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$,从而可判断f(x)在R上是增函数,故若x1≠x2,则$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0;作函数f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$的图象,由图象判断即可.
解答 解:f(x)=$\frac{x}{1+|x|}$,f(-x)=$\frac{-x}{1+|x|}$;
故等式f(-x)+f(x)=0在x∈R时恒成立,故①成立;
f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$,
故-1<f(x)<1,
故函数f(x)的值域为(-1,1),故②成立;
g(x)=f(x)-x=$\left\{\begin{array}{l}{\frac{-{x}^{2}}{1+x},x≥0}\\{\frac{{x}^{2}}{1-x},x<0}\end{array}\right.$,
故函数g(x)=f(x)-x在R上有一个零点,故③不成立;
∵f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$,
故可判断f(x)在R上是增函数,
故若x1≠x2,则$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
故④成立;
作函数f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{1-\frac{1}{1+x},x≥0}\\{-1+\frac{1}{1-x},x<0}\end{array}\right.$的图象如下,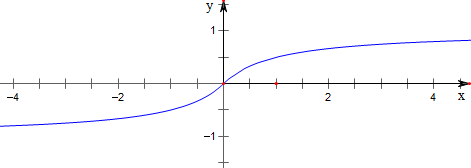
若0<x1<x2,则$\frac{f({x}_{1})+f({x}_{2})}{2}$$<f(\frac{{x}_{1}+{x}_{2}}{2})$,
若x1<x2<0,则$\frac{f({x}_{1})+f({x}_{2})}{2}$>f($\frac{{x}_{1}+{x}_{2}}{2}$).
故⑤不成立.
故答案为:①②④.
点评 本题考查了分段函数的应用及数形结合的思想的应用,属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 3x+y+3=0 | B. | 3x-y=0 | C. | 3x-y-3=0 | D. | 3x-y+3=0 |
| A. | 平面α的法向量垂直于与平面α共面的所有向量 | |
| B. | 一个平面的所有法向量互相平行 | |
| C. | 如果两个平面的法向量垂直,那么这两个平面也垂直 | |
| D. | 如果$\overrightarrow{a}$、$\overrightarrow{b}$与平面α共面且$\overrightarrow{n}$⊥$\overrightarrow{a}$,$\overrightarrow{n}$⊥$\overrightarrow{b}$,那么$\overrightarrow{n}$就是平面α的一个法向量 |
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上 如图所示,ABCD是矩形,平面ABCD与半圆O所在的平面垂直,E是半圆周上异于A,B的任意一点.
如图所示,ABCD是矩形,平面ABCD与半圆O所在的平面垂直,E是半圆周上异于A,B的任意一点.