题目内容
在△ABC中,不等式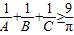 成立;在凸四边形ABCD中,不等式
成立;在凸四边形ABCD中,不等式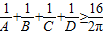 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式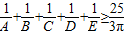 成立.根据以上情况,猜想在凸n边形A1A2…An(n≥3)中的成立的不等式是 .
成立.根据以上情况,猜想在凸n边形A1A2…An(n≥3)中的成立的不等式是 .
【答案】分析:根据已知中△ABC中,不等式 成立;在凸四边形ABCD中,不等式
成立;在凸四边形ABCD中,不等式 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式 成立.观察分子与多边形边的关系及分母中π的系数与多边形边的关系,即可得到答案.
成立.观察分子与多边形边的关系及分母中π的系数与多边形边的关系,即可得到答案.
解答:解:由已知中已知的多边形角的倒数所满足的不等式:
△ABC中,不等式 成立;
成立;
凸四边形ABCD中,不等式 成立;
成立;
凸五边形ABCDE中,不等式 成立;
成立;
…
由此推断凸n边形A1A2…An(n≥3)中的成立的不等式是:

故答案为:
点评:本题考查的知识点是归纳推理,其中根据已知分析分子与多边形边的关系及分母中π的系数与多边形边的关系,是解答本题的关键.
 成立;在凸四边形ABCD中,不等式
成立;在凸四边形ABCD中,不等式 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式 成立.观察分子与多边形边的关系及分母中π的系数与多边形边的关系,即可得到答案.
成立.观察分子与多边形边的关系及分母中π的系数与多边形边的关系,即可得到答案.解答:解:由已知中已知的多边形角的倒数所满足的不等式:
△ABC中,不等式
 成立;
成立;凸四边形ABCD中,不等式
 成立;
成立;凸五边形ABCDE中,不等式
 成立;
成立;…
由此推断凸n边形A1A2…An(n≥3)中的成立的不等式是:

故答案为:

点评:本题考查的知识点是归纳推理,其中根据已知分析分子与多边形边的关系及分母中π的系数与多边形边的关系,是解答本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
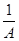 +
+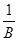 +
+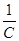 ≥
≥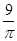 成立,在四边形ABCD中,不等式
成立,在四边形ABCD中,不等式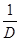 ≥
≥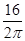 成立,在五边形ABCDE中,不等式
成立,在五边形ABCDE中,不等式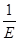 ≥
≥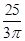 成立,猜想在n边形A1A2…An中,有不等式 (n≥3)成立.
成立,猜想在n边形A1A2…An中,有不等式 (n≥3)成立.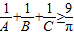 成立;在四边形ABCD中,不等式
成立;在四边形ABCD中,不等式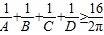 成立;在五边形ABCDE中,不等式
成立;在五边形ABCDE中,不等式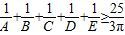 成立…,依此类推,在n边形A1A2…An中,不等式
成立…,依此类推,在n边形A1A2…An中,不等式 成立.
成立.