题目内容
用反证法证明圆的两条不是直径的相交弦不能互相平分.
思路分析:假设弦AB、CD被P平分,连结OP,由平面几何知识可推出OP⊥AB且OP⊥CD.又推出在平面内过一点P有两条直线AB和CD同时与OP垂直,这与垂线性质矛盾,则原命题成立.?
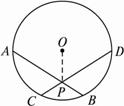
证明:已知:如图,在⊙O中弦AB、CD交于点P,且AB、CD不是直径.?
求证:弦AB、CD不被P平分.?
假设弦AB、CD被P平分,由于P点一定不是圆心O,连结OP,据垂径定理的推论,有OP⊥AB,OP⊥CD,?
即过点P有两条直线与OP都垂直,这与垂线性质矛盾.?
所以,弦AB、CD不被P平分.?
温馨提示:由上述例题可看出:利用反证法证明时,关键是从假设结论的反面出发,经过推理论证,得出可能与命题的条件,或者与已学过的定义、公理、定理等相矛盾的结论,这是由假设所引起的,因此假设是不正确的,从而肯定了命题结论的正确性.

练习册系列答案
相关题目