题目内容
用反证法证明：圆的两条不是直径的相交弦不能互相平分.
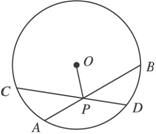
证明：如图所示，假设弦AB、CD被点P平分，由于P点一定不是圆心，连结OP，根据垂径定理的推论，有OP⊥CD,OP⊥AB，即过点P有两条直线与OP垂直，这与垂线性质矛盾，所以弦AB、CD不被P点平分.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
能考试期末冲刺卷系列答案题目内容
用反证法证明：圆的两条不是直径的相交弦不能互相平分.
证明：如图所示，假设弦AB、CD被点P平分，由于P点一定不是圆心，连结OP，根据垂径定理的推论，有OP⊥CD,OP⊥AB，即过点P有两条直线与OP垂直，这与垂线性质矛盾，所以弦AB、CD不被P点平分.
能考试期末冲刺卷系列答案