题目内容
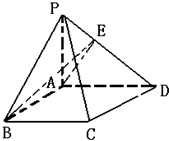
如图所示直角梯形ABCD中，∠A=90°，PA⊥面ABCD，AD||BC，AB=BC=a，AD=2a，与底面ABCD成30角．若AE⊥PD，E为垂足，PD与底面成30°角．（1）求证：BE⊥PD；
（2）求异面直线AE与CD所成的角的大小．
【答案】分析：（1）以A为原点，AB，AD，AP所在直线为坐标轴建立直角坐标系，根据向量数量积为零可知线线垂直，从而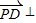 
面BEA，根据线面垂直的性质可知PD⊥BE；
（2）先分别求出向量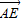
，向量 
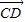的坐标，然后利用空间向量的夹角公式求出两向量的夹角的余弦值，即为AE与CD所成角的余弦值；
解答：
解：为了计算方便不妨设a=1．
（1）证明：根据题意可得：以A为原点，AB，AD，AP所在直线为坐标轴建立直角坐标系（如图）
则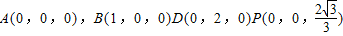
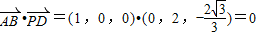
又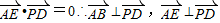
所以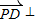
面BEA，BE?面BEA，
∴PD⊥BE
（2）∵PA⊥面ABCD，PD与底面成30°角，
∴∠PDA=30°
过E作EF⊥AD，垂足为F，则AE=AD•sin30°=1，∠EAF=60°
，
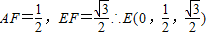于是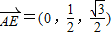
又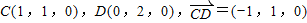
则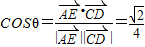
∴AE与CD所成角的余弦值为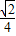
．
点评：本题主要考查了线线的位置关系、线线所成角，以及同时考查了利用空间向量求解立体几何问题，考查空间想象能力，运算求解能力，属于综合题．
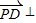面BEA，根据线面垂直的性质可知PD⊥BE；（2）先分别求出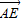向量
，向量 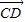的坐标，然后利用空间向量的夹角公式求出两向量的夹角的余弦值，即为AE与CD所成角的余弦值；解答：
解：为了计算方便不妨设a=1．（1）证明：根据题意可得：以A为原点，AB，AD，AP所在直线为坐标轴建立直角坐标系（如图）
则
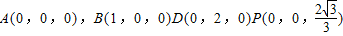
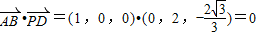
又
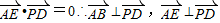
所以
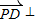面BEA，BE?面BEA，∴PD⊥BE
（2）∵PA⊥面ABCD，PD与底面成30°角，
∴∠PDA=30°
过E作EF⊥AD，垂足为F，则AE=AD•sin30°=1，∠EAF=60°
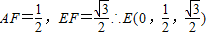，于是
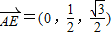
又
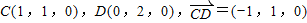
则
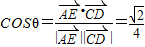
∴AE与CD所成角的余弦值为
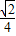．点评：本题主要考查了线线的位置关系、线线所成角，以及同时考查了利用空间向量求解立体几何问题，考查空间想象能力，运算求解能力，属于综合题．
练习册系列答案
相关题目
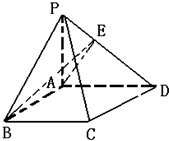如图所示直角梯形ABCD中，∠A=90°，PA⊥面ABCD，AD||BC，AB=BC=a，AD=2a，与底面ABCD成300角．若AE⊥PD，E为垂足，PD与底面成30°角．
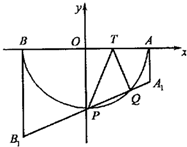已知T是半圆O的直径AB上一点，AB=2，OT=t（0＜t＜1）．以AB为腰的直角梯形AA1B1B中，AA1垂直于AT，且|AA1|=|AT|，BB1垂直于BT，且|BB1|=|BT|，A1B1交半圆于P，Q两点，建立如图所示直角坐标系，O为坐标原点．
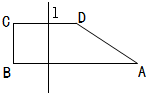如图所示直角梯形ABCD中上底CD=2，下底AB=4，高BC=1直线l与线段AB垂直相交，设A点到直线l的距离为x，直线l截梯形ABCD所得的位于l左方的图形面积为y．