题目内容
如图所示直角梯形ABCD中,∠A=90°,PA⊥面ABCD,AD||BC,AB=BC=a,AD=2a,与底面ABCD成300角.若AE⊥PD,E为垂足,PD与底面成30°角.
(1)求证:BE⊥PD;
(2)求异面直线AE与CD所成的角的大小.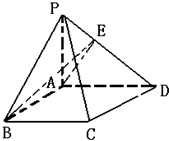
(1)求证:BE⊥PD;
(2)求异面直线AE与CD所成的角的大小.


为了计算方便不妨设a=1.
(1)证明:根据题意可得:以A为原点,AB,AD,AP所在直线为坐标轴建立直角坐标系(如图)
则 A(0,0,0),B(1,0,0)D(0,2,0)P(0,0,
2
| ||
| 3 |
| AB |
| PD |
2
| ||
| 3 |
又
| AE |
| PD |
| AB |
| PD |
| AE |
| PD |
所以
| PD |
∴PD⊥BE
(2)∵PA⊥面ABCD,PD与底面成30°角,
∴∠PDA=30°
过E作EF⊥AD,垂足为F,则AE=AD•sin30°=1,∠EAF=60°
AF=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
于是
| AE |
| 1 |
| 2 |
| ||
| 2 |
又 C(1,1,0),D(0,2,0),
| CD |
则 COSθ=
| ||||
|
|
| ||
| 4 |
∴AE与CD所成角的余弦值为
| ||
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
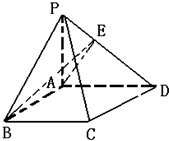 如图所示直角梯形ABCD中,∠A=90°,PA⊥面ABCD,AD||BC,AB=BC=a,AD=2a,与底面ABCD成300角.若AE⊥PD,E为垂足,PD与底面成30°角.
如图所示直角梯形ABCD中,∠A=90°,PA⊥面ABCD,AD||BC,AB=BC=a,AD=2a,与底面ABCD成300角.若AE⊥PD,E为垂足,PD与底面成30°角.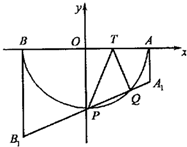 已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.
已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.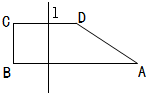 如图所示直角梯形ABCD中上底CD=2,下底AB=4,高BC=1直线l与线段AB垂直相交,设A点到直线l的距离为x,直线l截梯形ABCD所得的位于l左方的图形面积为y.
如图所示直角梯形ABCD中上底CD=2,下底AB=4,高BC=1直线l与线段AB垂直相交,设A点到直线l的距离为x,直线l截梯形ABCD所得的位于l左方的图形面积为y.