题目内容
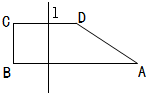 如图所示直角梯形ABCD中上底CD=2,下底AB=4,高BC=1直线l与线段AB垂直相交,设A点到直线l的距离为x,直线l截梯形ABCD所得的位于l左方的图形面积为y.
如图所示直角梯形ABCD中上底CD=2,下底AB=4,高BC=1直线l与线段AB垂直相交,设A点到直线l的距离为x,直线l截梯形ABCD所得的位于l左方的图形面积为y.(1)求函数y=f(x)解析式;
(2)在给定的坐标系内画出y=f(x)的图象.
分析:讨论直线l的位置,建立对应图形的关系,进行求函数解析式即可.
解答: 解:(1)在直角梯形ABCD中上底CD=2,下底AB=4,高BC=1,
解:(1)在直角梯形ABCD中上底CD=2,下底AB=4,高BC=1,
∴AE=4-2=2,DE=1,tan∠DAE=
.
若0≤x≤2,此时AF=x,GF=
,三角形GAF的面积为
x•
=
,
∴f(x)=
-
=3-
,(0≤x≤2).
当2<x≤4时,此时AG=x,BG=4-x,
此时f(x)=(4-x)×1=4-x,(2<x≤4),
∴f(x)=
(2)在坐标系中作出函数f(x)的图象如图:
 解:(1)在直角梯形ABCD中上底CD=2,下底AB=4,高BC=1,
解:(1)在直角梯形ABCD中上底CD=2,下底AB=4,高BC=1,∴AE=4-2=2,DE=1,tan∠DAE=
| 1 |
| 2 |
若0≤x≤2,此时AF=x,GF=
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x2 |
| 4 |
∴f(x)=
| (2+4)×1 |
| 2 |
| x2 |
| 4 |
| x2 |
| 4 |
当2<x≤4时,此时AG=x,BG=4-x,

此时f(x)=(4-x)×1=4-x,(2<x≤4),
∴f(x)=
|
(2)在坐标系中作出函数f(x)的图象如图:
点评:本题主要考查函数的应用,利用分段函数建立函数关系即可.

练习册系列答案
相关题目
 如图所示直角梯形ABCD中,∠A=90°,PA⊥面ABCD,AD||BC,AB=BC=a,AD=2a,与底面ABCD成300角.若AE⊥PD,E为垂足,PD与底面成30°角.
如图所示直角梯形ABCD中,∠A=90°,PA⊥面ABCD,AD||BC,AB=BC=a,AD=2a,与底面ABCD成300角.若AE⊥PD,E为垂足,PD与底面成30°角.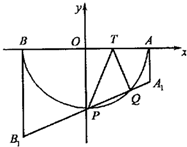 已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.
已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.