题目内容
(本小题12分) 已知p: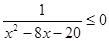 ,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
解析试题分析:由命题p成立求得x的范围为A,由命题q成立求得x的范围为B,由题意可得A?B,可得,由此求得 ,实数m的取值范围.
,实数m的取值范围.
解: “┐p”: 0, 解集A={x|x
0, 解集A={x|x 10或x
10或x
由q:x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴“┐q”:B={x|x>1+m或x<1-m,m>0
由“┐p”是“┐q”的必要而不充分条件可知:B A.故
A.故  , 解得m
, 解得m 9.
9.
考点:本题主要考查了分式不等式的解法,充分条件、必要条件、充要条件的定义,体现了等价转化的数学思想,属于中档题.
点评:解决该试题的关键是由命题p成立求得x的范围为A,由命题q成立求得x的范围为B,由题意可得A?B,可得。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
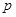 :方程
:方程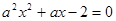 在[-1,1]上有解;命题
在[-1,1]上有解;命题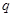 :只有一个实数
:只有一个实数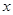 满足不等式
满足不等式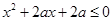 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围. :方程
:方程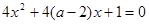 无实数根;命题
无实数根;命题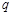 :函数
:函数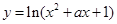 的值是
的值是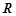 .如果命题
.如果命题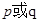 为真命题,
为真命题,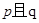 为假命题,求实数
为假命题,求实数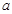 的取值范围。
的取值范围。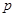 :“
:“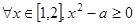 ”,命题
”,命题 :“
:“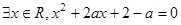 ”,若命题“
”,若命题“ ”是真命题,求实数
”是真命题,求实数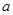 的取值范围。
的取值范围。 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,
轴上的双曲线, :方程
:方程 =(
=( 一
一 )
)

 ,其中
,其中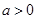 ,命题
,命题 实数
实数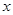 满足
满足 .
. 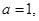 且
且 为真,求实数
为真,求实数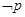 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.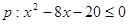 ,
,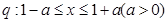 ,若非
,若非 是非
是非 的充分不必要条件,求
的充分不必要条件,求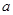 的取值范围。
的取值范围。 :关于
:关于 的方程
的方程 有实数解;命题
有实数解;命题 :
: .
.