题目内容
(本小题满分12分)已知 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,
轴上的双曲线, :方程
:方程 =(
=( 一
一 )
) 表示开口向右的抛物线.若“
表示开口向右的抛物线.若“

 ”为真命题,“
”为真命题,“

 ”为假命题,求实数
”为假命题,求实数 的范围.
的范围.

解析试题分析:由题意可知命题P,命题q,为真时对应的参数a的范围,然后利用,“

 ”为真命题,“
”为真命题,“

 ”为假命题,说明一真一假,进而分类讨论得到参数a的范围。
”为假命题,说明一真一假,进而分类讨论得到参数a的范围。
解: 为真时,
为真时, ;
; 为真时,
为真时, ,得
,得 ;
;
当 为真,
为真, 为假时,
为假时, 无值;当
无值;当 为假,
为假, 为真时,
为真时, 。
。
∴ 的取值范围是
的取值范围是
考点:本题主要考查双曲线和抛物线的方程的理解和运用,以及命题的真值问题。
点评:解决该试题的关键是能通过已知中焦点的位置,得到参数a的范围,同时利用或命题一真即真,且命题,一假即假,;来分情况讨论得到。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
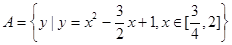 ,
,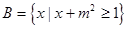 .命题
.命题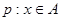 ,命题
,命题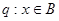 ,且命题
,且命题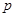 是命题
是命题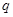 的充分条件,求实数
的充分条件,求实数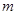 的取值范围.
的取值范围.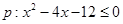 ,
,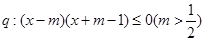 ,且
,且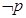 是
是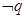 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.  ,
, ,若
,若 是
是 充分条件,求实数m的取值范围.
充分条件,求实数m的取值范围. ,
, ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.)
的取值范围.)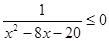 ,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围. .若q成立的一个充分不必要条件是p,求实数
.若q成立的一个充分不必要条件是p,求实数 的取值范围.
的取值范围. ,命题
,命题 :
: 在区间
在区间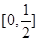 上为减函数;命题
上为减函数;命题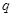 :方程
:方程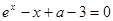 在
在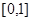 有解。若
有解。若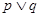 为真,
为真,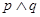 为假,求实数
为假,求实数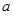 的取值范围。
的取值范围。 ,
,
