题目内容
5. 如图,在△OAB中,C、D分别为AB、OB的中点,E为OA上离点O最近的四等分点,F为CE与AD的交点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{OF}$=( )
如图,在△OAB中,C、D分别为AB、OB的中点,E为OA上离点O最近的四等分点,F为CE与AD的交点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{OF}$=( )| A. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{3}{10}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$ | C. | $\frac{1}{5}$$\overrightarrow{a}$+$\frac{3}{10}$$\overrightarrow{b}$ | D. | $\frac{3}{5}$$\overrightarrow{a}$+$\frac{3}{10}$$\overrightarrow{b}$ |
分析 首先根据在△OAB中,C、D分别为AB、OB的中点,E为OA上离点O最近的四等分点,得到CD与OA的长度的关系,进一步得到向量的线性关系,利用三角形法则运算,得到所求.
解答 解:在△OAB中,C、D分别为AB、OB的中点,E为OA上离点O最近的四等分点,所以$\frac{CD}{AE}=\frac{\frac{1}{2}OA}{\frac{3}{4}OA}=\frac{2}{3}$,
所以$\overrightarrow{OF}=\overrightarrow{OE}+\overrightarrow{EF}$=$\frac{1}{4}\overrightarrow{OA}+\frac{3}{5}\overrightarrow{EC}$=$\frac{1}{4}\overrightarrow{OA}+\frac{3}{5}(\overrightarrow{EA}+\overrightarrow{AC})$=$\frac{1}{4}\overrightarrow{OA}+\frac{3}{5}(\frac{3}{4}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{AB})$=$\frac{1}{4}\overrightarrow{OA}+\frac{9}{20}\overrightarrow{OA}+\frac{3}{10}(\overrightarrow{OB}-\overrightarrow{OA})$=$\frac{2}{5}\overrightarrow{OA}+\frac{3}{10}\overrightarrow{OB}$=$\frac{2}{5}\overrightarrow{a}+\frac{3}{10}\overrightarrow{b}$;
故选:A.
点评 本题考查了平面向量加减法的三角形法则的运用;要充分利用C、D分别为AB、OB的中点,E为OA上离点O最近的四等分点,得到向量之间的关系.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数$\overline{x}$ | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
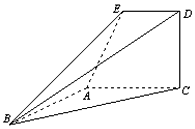 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE. 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)