题目内容
椭圆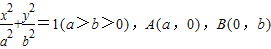 ,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e= .
,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e= .
【答案】分析:确定直线AB的方程为:bx+ay-ab=0,利用原点到过A(a,0),B(0,b)两点的直线的距离是c,建立方程,即可求得椭圆的离心率.
解答:解:由题意,直线AB的方程为:bx+ay-ab=0
∵原点到过A(a,0),B(0,b)两点的直线的距离是c
∴ =c
=c
∴a2b2=c2(a2+b2)
∴a2(a2-c2)=c2(2a2-c2)
∴e4-3e2+1=0
∴e=
故答案为:
点评:本题考查椭圆的性质,主要考查求椭圆的离心率,考查计算能力,属于基础题.
解答:解:由题意,直线AB的方程为:bx+ay-ab=0
∵原点到过A(a,0),B(0,b)两点的直线的距离是c
∴
 =c
=c∴a2b2=c2(a2+b2)
∴a2(a2-c2)=c2(2a2-c2)
∴e4-3e2+1=0
∴e=

故答案为:

点评:本题考查椭圆的性质,主要考查求椭圆的离心率,考查计算能力,属于基础题.

练习册系列答案
相关题目
 ,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e=________.
,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e=________.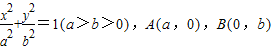 ,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e= .
,原点到直线AB的距离为c(c为半焦距),则椭圆离心率e= .