Question

【题目】在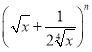的展开式中，前3项的系数成等差数列，

（1）求的值；

（2）求展开式中二项式系数最大的项及各项系数和；

（3）求展开式中含的项的系数及有理项.

Answer 1

【答案】（1）（2）最大的项为第五项，；（3）；；；．

【解析】

（1）根据前3项的系数成等差数列，利用等差数列的定义求得的值；

（2）根据通项公式、二项式系数的性质求展开式中二项式系数最大的项，令即可求得展开式系数和；

（3）在二项展开式的通项公式中，令的幂指数等于，求出的值，即可求得含的项的系数．设展开式中第项为有理项，则，当、4、8时对应的项为有理项．

解：（1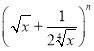）展开式的通项为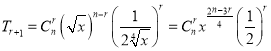

因为前3项的系数成等差数列，且前三项系数为，

所以，即，

所以（舍去）或.

（2）因为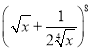，所以展开式中二项式系数最大的项为第五项，

即.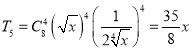

令得，即展开式系数和为

（3）通项公式：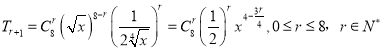

由，，

可得含的项的系数为.

设展开式中第项为有理项，由

当、4、8时对应的项为有理项，有理项分别为：；；．