题目内容
直线(2k-1)x-(k+3)y-(k-11)=0(k∈R)所经过的定点是
- A.(5,2)
- B.(2,3)
- C.(-
 ,3)
,3) - D.(5,9)
B
分析:直线方程即(2x-y-1)•k-(x+3y-11)=0,根据直线经过的定点的坐标满足 ,求出定点的坐标.
,求出定点的坐标.
解答:由(2k-1)x-(k+3)y-(k-11)=0,得(2x-y-1)•k-(x+3y-11)=0.
所以直线经过的定点的坐标满足 ,
,
联立方程组解得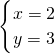 ,
,
故直线所经过的定点是(2,3),
故选B.
点评:本题主要考查直线过定点问题,利用了直线(ax+by+c)+k•(a′x+b′y+c′)=0经过的定点坐标是方程组
 的解,属于中档题.
的解,属于中档题.
分析:直线方程即(2x-y-1)•k-(x+3y-11)=0,根据直线经过的定点的坐标满足
 ,求出定点的坐标.
,求出定点的坐标.解答:由(2k-1)x-(k+3)y-(k-11)=0,得(2x-y-1)•k-(x+3y-11)=0.
所以直线经过的定点的坐标满足
 ,
,联立方程组解得
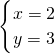 ,
,故直线所经过的定点是(2,3),
故选B.
点评:本题主要考查直线过定点问题,利用了直线(ax+by+c)+k•(a′x+b′y+c′)=0经过的定点坐标是方程组
 的解,属于中档题.
的解,属于中档题. 
练习册系列答案
相关题目
不论k为何值,直线(2k-1)x-(k-2)y-(k+4)=0恒过的一个定点是( )
| A、(0,0) | B、(2,3) | C、(3,2) | D、(-2,3) |