已知集合A={(x.y)|y=x2}.B={(x.y)|2x-y-1=0}.则A∩B=( )A．x=1.y=1B．(1.1)C．{1.1}D．{(1.1)} 题目和参考答案——青夏教育精英家教网—

题目内容

6．已知集合A={（x，y）|y=x²}，B={（x，y）|2x-y-1=0}，则A∩B=（　　）

A．

x=1，y=1

B．

（1，1）

C．

{1，1}

D．

{（1，1）}

分析联立A与B中两方程组成方程组，求出方程组的解即可确定出两集合的交集．

解答解：联立得：$\left\{\begin{array}{l}{y={x}^{2}}\\{2x-y-1=0}\end{array}\right.$，
消去y得：2x-1=x²，即（x-1）²=0，
解得：x=1，y=1，
则A∩B={（1，1）}，
故选：D．

点评此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案

相关题目

2．函数y=log₂x（x≥1）的反函数是y=2^x（x≥0）．

3．已知3$\overrightarrow{a}$-2$\overrightarrow{b}$=（-2，0，4），$\overrightarrow{c}$=（-2，1，2），$\overrightarrow{a}$•$\overrightarrow{c}$=2，且|$\overrightarrow{b}$|=4．
（1）求cos＜$\overrightarrow{b}$，$\overrightarrow{c}$＞；
（2）记$\overrightarrow{d}$=（-2，0，4），确定实数k，使得（$\overrightarrow{d}$+k$\overrightarrow{c}$）与（$\overrightarrow{d}$-2$\overrightarrow{c}$）互相垂直．

20．

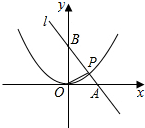如图，直线l经过A（4，0）和B（0，4）两点，它与抛物线y=ax²在第一象限内交于P点，如果△AOP的面积为2，求此抛物线的解析式．

1．已知抛物线C₁：y²=2px（p＞0）的焦点为F，抛物线上的点G（1，m）到焦点的距离为3，椭圆C₂：$\frac{x^2}{m^2}+\frac{y^2}{n^2}$=1（m＞n＞0）的一个焦点与抛物线C₁的焦点重合，且离心率为$\frac{1}{2}$．
（1）求抛物线C₁和椭圆C₂的方程；
（2）已知直线l：y=kx-4交椭圆C₂于A、B两个不同的点，若原点O在以线段AB为直径的圆的外部，求k的取值范围．

11．已知抛物线C：y²=4x
（1）抛物线C上有一动点P，当P到C的准线与到点Q（7，8）的距离之和最小时，求点P的坐标；
（2）是否存在直线l：y=kx+b与C交于A、B两个不同的点，使OA与OB（O为坐标原点）所在直线的倾斜角互补，如果存在，试确定k与b的关系，如果不存在，请说明理由．

18．已知集合A={x|y=log₂（4-x²）}，B={y|y=2^x+1}，则A∩B=（　　）

15．已知命题p：?m∈R，使得函数f（x）=x²+（m-1）x²-2是奇函数，命题q：向量$\overrightarrow{a}$=（x₁，y₁），$\overrightarrow{b}$=（x₂，y₂），则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是：“$\overrightarrow{a}$$∥\overrightarrow{b}$”的充要条件，则下列命题为真命题的是（　　）

16．f（x）=cosx+sinx的最大值为$\sqrt{2}$．

试题分类