题目内容
不等式|x+1|+1＞0的解集是（ ）
| A、R | B、∅ |
| C、（0，2） | D、（-1，1） |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：要解的不等式即|x+1|＞-1，显然恒成立，从而得到它的解集．
解答：
解：由不等式|x+1|+1＞0可得，|x+1|＞-1，显然恒成立，
故不等式的解集为R，
故选：A．
故不等式的解集为R，
故选：A．
点评：本题主要考查绝对值的意义，属于基础题．
练习册系列答案
相关题目
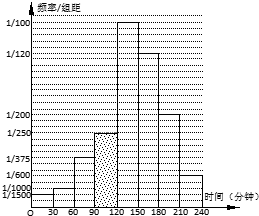为了调查学生星期天晚上学习时间利用问题，某校从高二年级100名学生（其中走读生450名，住宿生550名）中，采用分层抽样的方法抽取n名学生进行问卷调查，根据问卷取得了这n名同学每天晚上学习时间（单位：分钟）的数据，按照以下区间分为八组已知奇函数f（x）在R上单调递增，若f（sin2θ）+f（2mcosθ+m）＞0对任意θ∈[-
，
]恒成立，则实数m的范围为（ ）
| π |
| 3 |
| π |
| 3 |
A、-
| ||
B、m＞-
| ||
| C、m＞0 | ||
| D、m＞1 |