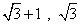题目内容
已知f(x)=lnx,g(x)=af(x)+f′(x),
(1)求g(x)的单调区间;
(2)当a=1时, ①比较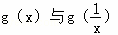 的大小;
的大小;
②是否存在x0>0,使得|g(x)﹣g(x0)|<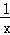 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
【解析】 ,
,
g(x)的定义域为(0,+∞).

①当a≤0时,g'(x)<0,(0,+∞)是g(x)的单调区间;
②当a>0时,由g'(x)>0,得 ;由g'(x)<0,得
;由g'(x)<0,得 ,
,
即增区间是 ,减区间是
,减区间是 .
.
(2) ,
,
∴

①当x=1时,μ(x)=0,此时
②当0<x<1时,μ'(x)<0,∴μ(x)>μ(1)=0.∴
③当x>1时,μ'(x)<0,∴μ(x)<μ(1)=0.∴ .
.
(3) ⇔
⇔
⇔
∵lnx∈(0,+∞),∴g(x0)>lnx不能恒成立.
故x0不存在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=ln(ex﹣1)(x>0)( )
|
| A. | 若f(a)+2a=f(b)+3b,则a>b | B. | 若f(a)+2a=f(b)+3b,则a<b |
|
| C. | 若f(a)﹣2a=f(b)﹣3b,则a>b | D. | 若f(a)﹣2a=f(b)﹣3b,则a<b |
 与
与 呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )
呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( ) .
.
 .
.
 .
.
 .
.

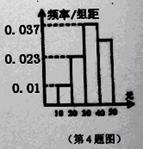
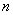 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在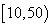 (单位:元),其中支出在
(单位:元),其中支出在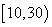 (单位:元)的同学有
(单位:元)的同学有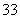 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在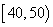 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )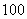 B.
B.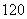 C.
C.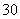 D.
D.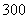
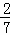 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数. 在
在 上的图象是( )
上的图象是( )
 上的函数
上的函数 满足
满足 ,若
,若 ,则
,则
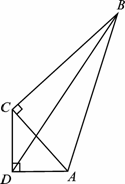
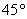 的直角三角板ADC和
的直角三角板ADC和 的直角三角板ABC拼在一起组成平面四边形ABCD,其中
的直角三角板ABC拼在一起组成平面四边形ABCD,其中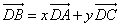 ,则x,y分别等于( )
,则x,y分别等于( )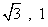 B.
B.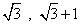 C.
C.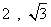 D.
D.