题目内容
根据下列条件求双曲线的标准方程．
与椭圆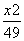
＋
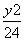＝1有公共焦点，且离心率e＝
.
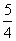解法1(设标准方程)
由椭圆方程可得焦点坐标为(－5,0)，(5,0)，
即c＝5且焦点在x轴上，
∴可设双曲线的标准方程为
－
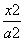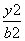＝1(a>0，b>0)，且c＝5.
又e＝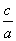
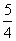＝，∴a＝4，∴b2＝c2－a2＝9.
∴双曲线的标准方程为
－
＝1.
解法2(设共焦点双曲线系方程)
∵椭圆的焦点在x轴上，
∴双曲线的标准方程为－＝1.
练习册系列答案
相关题目
题目内容
根据下列条件求双曲线的标准方程．
与椭圆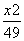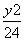＋＝1有公共焦点，且离心率e＝.
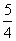解法1(设标准方程)
由椭圆方程可得焦点坐标为(－5,0)，(5,0)，
即c＝5且焦点在x轴上，
∴可设双曲线的标准方程为
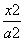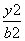－＝1(a>0，b>0)，且c＝5.
又e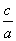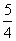＝＝，∴a＝4，∴b2＝c2－a2＝9.
∴双曲线的标准方程为－＝1.
解法2(设共焦点双曲线系方程)
∵椭圆的焦点在x轴上，
∴双曲线的标准方程为－＝1.
，在y轴上截得线段长为2
.
，求圆P的方程．
·
＝0，则|
B．2
D．2