题目内容
1.已知:点E(1,0),点A在直线l1:x-y+1=0上运动,过点A,E的直线l与直线l2:x+y+1=0交于点B,线段AB的中点M在一个曲线上运动,则这个曲线的方程是x2-y2=1.分析 设A(a,a+1),则直线AE的方程为y=$\frac{a+1}{a-1}$(x-1),与直线l2:x+y+1=0联立,可得B的坐标,进而可得线段AB的中点M的坐标,消去a,即可得到结论.
解答 解:设A(a,a+1),则直线AE的方程为y=$\frac{a+1}{a-1}$(x-1),
与直线l2:x+y+1=0联立,可得B($\frac{1}{a}$,-$\frac{1}{a}$-1),
设M(x,y),则x=$\frac{1}{2}$(a+$\frac{1}{a}$),y=$\frac{1}{2}$(a-$\frac{1}{a}$),
消去a,可得x2-y2=1.
故答案为:x2-y2=1.
点评 本题考查曲线方程,考查学生的计算能力,正确求出B的坐标是关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
16.已知复数z,“z+$\overline{z}$=0”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也不必要条件 |
11.设集合M={1,2,3},N={1,2},则M∩N等于( )
| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {1,2,3} |
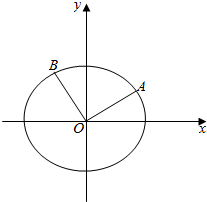 如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.
如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.