题目内容
已知函数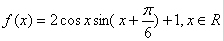 .
.
(Ⅰ)求函数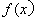 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)若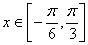 ,求函数的值域.
,求函数的值域.
解:(Ⅰ)f(x)=cos x(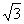 sin x+cos x)+1
sin x+cos x)+1
=cos2x+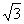 sin x cos x+1
sin x cos x+1
=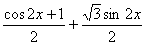 +1
+1
=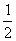 cos2x+
cos2x+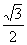 sin2x+
sin2x+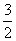
=sin(2x+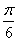 )+
)+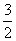
∵T=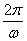 =
=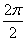 =
=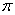
即函数f(x)的最小正周期为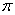 .
.
由f(x)=sin(2x+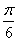 )+
)+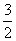
由2k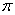 -
-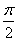 ≤2x+
≤2x+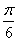 ≤2k
≤2k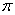 +
+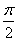 ,
,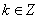
解得:-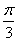 +k
+k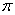 ≤x≤
≤x≤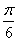 +k
+k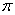 ,
, 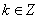
故函数f(x)=sin(2x+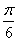 )+
)+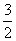 的单调递增区间为[-
的单调递增区间为[-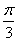 +k
+k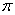 ,
,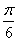 +k
+k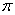 ],
],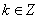 。
。
(Ⅱ)x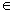 [-
[-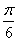 ,
, 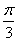 ] , -
] , -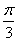 ≤2x≤
≤2x≤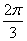 ,-
,-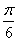 ≤2x+
≤2x+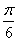 ≤
≤
∴-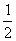 ≤sin(2x+
≤sin(2x+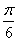 )≤1
)≤1
∴1≤sin(2x+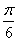 )+
)+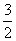 ≤
≤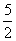
∴函数的值域为[1, 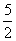 ].
].

练习册系列答案
相关题目
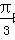 时取得最小值-4.
时取得最小值-4.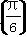 ,求数列
,求数列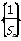 的前n项和Tn.
的前n项和Tn.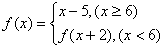 ,则f(3)为( )
,则f(3)为( )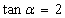 ,则
,则 __________.
__________. ,直线
,直线 ,则
,则 与
与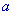 的位置关系是( )
的位置关系是( ) 的体积为V,点P、Q分别在侧棱
的体积为V,点P、Q分别在侧棱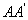 和
和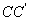 上,AP=
上,AP=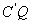 ,则四棱锥B—APQC的体积为( )
,则四棱锥B—APQC的体积为( ) B、
B、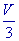 C、
C、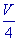 D、
D、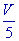

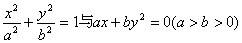 的曲线大致是 ( )
的曲线大致是 ( )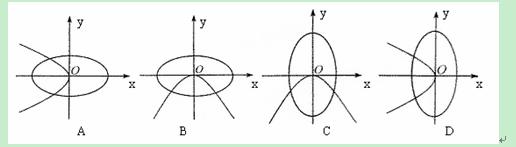
 左支上一点P到其左、右两焦点F1、F2的距离之和为8,
左支上一点P到其左、右两焦点F1、F2的距离之和为8,