题目内容
已知函数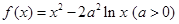 .
.
(Ⅰ)求函数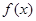 的单调区间;
的单调区间;
(Ⅱ)记函数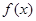 的最小值为
的最小值为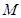 ,求证:
,求证: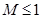 .
.
(Ⅰ)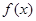 的单调递增区间为
的单调递增区间为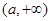 ;
;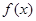 的单调递减区间为
的单调递减区间为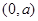 ;
;
(Ⅱ)详见解析
解析试题分析:(Ⅰ)先求导,再令导数等于0,讨论导数的正负得函数的增减区间。(Ⅱ)由(Ⅰ)知,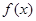 的最小值
的最小值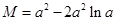 .令
.令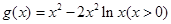 还是先求导再令导数等于0,讨论导数的正负得函数
还是先求导再令导数等于0,讨论导数的正负得函数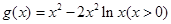 的单调区间,从而可求得此函数的最值。
的单调区间,从而可求得此函数的最值。
试题解析:解: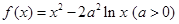 的定义域为
的定义域为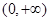 .
.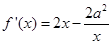
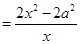
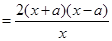 . 2分
. 2分
令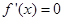 ,解得
,解得 或
或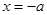 (舍).
(舍).
当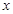 在
在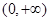 内变化时,
内变化时,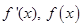 的变化情况如下:
的变化情况如下: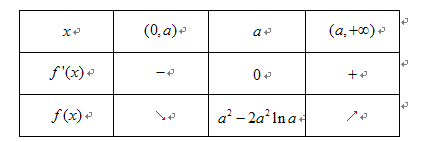
由上表知,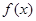 的单调递增区间为
的单调递增区间为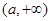 ;
;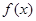 的单调递减区间为
的单调递减区间为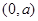 .
.
5分
(Ⅱ)由(Ⅰ)知,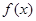 的最小值
的最小值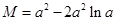 . 6分
. 6分
令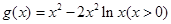 ,则
,则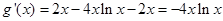 .
.
令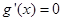 ,解得
,解得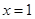 . 8分
. 8分
当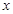 在
在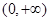 内变化时,
内变化时,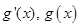 的变化情况如下:
的变化情况如下:
所以函数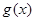 的最大值为
的最大值为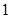 ,即
,即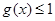 .
.
因为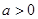 ,所以
,所以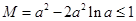 . 11分
. 11分
考点:1导数;2利用导数判断函数的单调性;3利用单调性求最值。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 在
在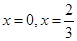 处存在极值.
处存在极值.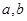 的值;
的值;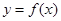 的图像上存在两点A,B使得
的图像上存在两点A,B使得 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在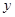 轴上,求实数
轴上,求实数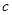 的取值范围;
的取值范围;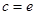 时,讨论关于
时,讨论关于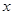 的方程
的方程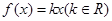 的实根个数.
的实根个数.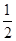 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*)..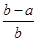 <ln
<ln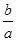 <
<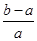 ,其中0<a<b;
,其中0<a<b; + +
+ + ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).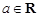 ,函数
,函数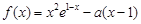 .
.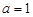 时,求
时,求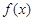 在
在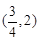 内的极大值;
内的极大值;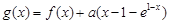 ,当
,当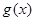 有两个极值点
有两个极值点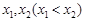 时,总有
时,总有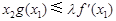 ,求实数
,求实数 的值.(其中
的值.(其中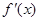 是
是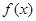 的导函数.)
的导函数.)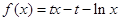
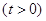 .
. 在
在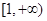 上为增函数,求实数
上为增函数,求实数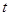 的取值范围;
的取值范围;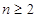 且
且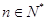 时,证明:
时,证明: 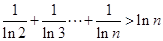 .
.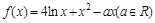 .
.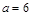 时,求函数
时,求函数 的单调区间;
的单调区间;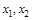 ,且
,且 ,求证:
,求证: ;
;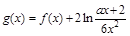 ,对于任意
,对于任意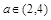 时,总存在
时,总存在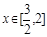 ,使
,使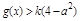 成立,求实数
成立,求实数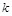 的取值范围.
的取值范围. ,
,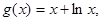 其中
其中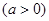
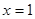 是函数
是函数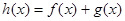 的极值点,求实数
的极值点,求实数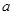 的值;
的值;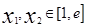 (
(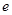 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数