题目内容
已知函数![]()
(Ⅰ)若![]() ,求函数
,求函数![]()
![]() 的极值和单调区间;
的极值和单调区间;
(II) 若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
解:(I)因为![]() , …………………2分
, …………………2分
当![]() ,
, ![]() ,
,
令![]() ,得
,得 ![]() , …………………3分
, …………………3分
又![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
|
|
|
| 极小值 |
|
所以![]() 时,
时,![]() 的极小值为1 . …………………5分
的极小值为1 . …………………5分
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ; …………………6分
; …………………6分
(II)解法一:
因为![]() ,且
,且![]() ,
,
令![]() ,得到
,得到![]() ,
,
若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
其充要条件是![]() 在区间
在区间![]() 上的最小值小于0即可. …………………7分
上的最小值小于0即可. …………………7分
(1)当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 成立,
成立,
所以,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() …………………9分
…………………9分
(2)当![]() ,即
,即![]() 时,
时,
① 若![]() ,则
,则![]() 对
对![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于0不成立 …………………11分
上的最小值小于0不成立 …………………11分
② 若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,
,
得 ![]() ,解得
,解得![]() ,即
,即![]() . …………………13分
. …………………13分
综上,由(1)(2)可知:![]() 符合题意. …………………14分
符合题意. …………………14分
解法二:若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立, 即
成立, 即![]() ,
,
因为![]() , 所以,只需
, 所以,只需![]() …………………7分
…………………7分
令![]() ,只要
,只要![]() 在区间
在区间![]() 上
上![]() 的最小值小于0即可
的最小值小于0即可
因为![]() ,
,
令![]() ,得
,得![]() …………………9分
…………………9分
(1)当![]() 时:
时:
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
|
因为![]() 时,
时,![]() ,而
,而![]() ,
,
只要![]() ,得
,得![]() ,即
,即![]() …………………11分
…………………11分
(2)当![]() 时:
时:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以,当 ![]() 时,
时,![]() 极小值即最小值为
极小值即最小值为![]() ,
,
由![]() , 得
, 得 ![]() ,即
,即![]() . …………………13分
. …………………13分
综上,由(1)(2)可知,有![]() . …………………14分
. …………………14分

 ,
, 
 .
. , 函数
, 函数 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围; 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点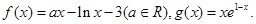
 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值; ,都有唯一的
,都有唯一的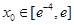 ,使得
,使得 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。
 ,求
,求 的单调递减区间;
的单调递减区间; ,求
,求 的最小值;
的最小值; ,且存在
,且存在 使得
使得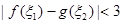 ,求实数
,求实数 的取值范围。
的取值范围。 .
. ,求函数
,求函数 在区间
在区间 的值域;
的值域; 上为增函数,求
上为增函数,求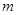 的取值范围.
的取值范围.