题目内容
如图1-4-9,△ABC中,∠ABC=90°,BD⊥AC于D,BC =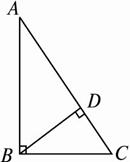
cm,BD =4 cm,求S△BDA∶S△CDB.
图1-4-9
思路分析:求S△BDA∶S△CDB?,实际上是求AD∶DC,显然结合已知条件,应用射影定理,不难求出AD、DC的长度.
解:∵BD⊥AC, 
cm,BD =4 cm,?
∴由勾股定理得DC =2 cm.?
在△ABC中,∠ABC=90°,BD⊥AC.?
∴由射影定理得BD2=AD·DC.?
∴ =
.?
∴S△BDA∶S△CDB =AD∶DC =8∶2 =4∶1.
练习册系列答案
相关题目
,θA)、B(25,π-arctan
,θB)，求出这两个截面间的距离.
用红、黄、蓝三种颜色之一去涂图中标号为
的
个小正方形（如图1），使得任意相邻（有公共边的）小正方形所涂颜色都不相同，且标号为“
、
、”的小正方形涂相同的颜色，则符合条件的所有涂法共有（ ）
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
A．
种 B．
种 C．
种 D．
种
,
)，该导弹运行与地面最大高度为3千米，相应水平距离为4千米(即图中E点)，在地面O、A两个观测点测得空中固定目标C的仰角分别为α和β，tanα=
，tanβ=
，不考虑空气阻力，导弹飞行轨道为一抛物线，那么按轨道运行的导弹能否击中目标C?说明理由.