题目内容
13.已知函数f(x)=cosxcos(x+$\frac{π}{3}$),求函数f(x)的最小正周期.分析 首先,化简函数解析式,然后,根据周期公式确定其周期公式即可.
解答 解:f(x)=cosxcos(x+$\frac{π}{3}$)
=cosx(cosxcos$\frac{π}{3}$-sinxsin$\frac{π}{3}$)
=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sinxcosx
=$\frac{1}{2}$×$\frac{1+cos2x}{2}$-$\frac{\sqrt{3}}{4}$sin2x
=$\frac{1}{4}$cos2x-$\frac{\sqrt{3}}{4}$sin2x+$\frac{1}{4}$
=$\frac{1}{2}$cos(2x+$\frac{π}{3}$)+$\frac{1}{4}$,
∴f(x)=$\frac{1}{2}$cos(2x+$\frac{π}{3}$)+$\frac{1}{4}$,
∴周期T=$\frac{2π}{2}$=π.
点评 本题重点考查了二倍角公式、辅助角公式、周期公式等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.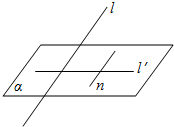 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
(1)cos<l,n>=cos<l,l′>•cos<l′,n>;
(2)n⊥l?n⊥l′.
 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:(1)cos<l,n>=cos<l,l′>•cos<l′,n>;
(2)n⊥l?n⊥l′.
2.已知函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列判断正确的是( )


| A. | a<0,b<0,c<0 | B. | a>0,b>0,c<0 | C. | a>0,b<0,c>0 | D. | a>0,b>0,c>0 |
 .
. ;
; ,若
,若 ,求实数
,求实数 的取值集合.
的取值集合.