题目内容
已知函数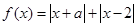
(I)当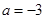 时,求不等式
时,求不等式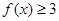 的解集;
的解集;
(Ⅱ)若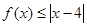 的解集包含
的解集包含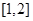 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)将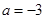 带入绝对值不等式,按
带入绝对值不等式,按 ,
, ,
, 分类讨论,(2)将题中的不等式问题转化成恒成立问题,再根据恒成立问题进行求解.
分类讨论,(2)将题中的不等式问题转化成恒成立问题,再根据恒成立问题进行求解.
试题解析:(1)当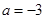 时,
时,
 或
或 或
或
 或
或
或解利用绝对值的几何意义求解, 表示数轴上变量
表示数轴上变量 到3的距离,
到3的距离, 表示数轴上变量
表示数轴上变量 到2的距离,
到2的距离, 表示数轴上变量
表示数轴上变量 到2和3的距离之和大于等于3,由图可知
到2和3的距离之和大于等于3,由图可知 或
或 .
.
(2)原命题 在
在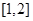 上恒成立
上恒成立 在
在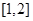 上恒成立
上恒成立 在
在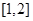 上恒成立
上恒成立
考点:绝对值不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
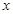 的不等式
的不等式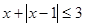 ;
;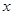 的不等式
的不等式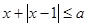 有解,求实数
有解,求实数 的取值范围.
的取值范围.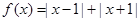 .
.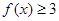 的解集;
的解集; 的不等式
的不等式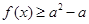 在
在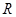 上恒成立,求实数
上恒成立,求实数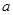 的取值范围.
的取值范围.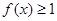 在区间(-∞,+∞)上恒成立,求实数a的取值范围
在区间(-∞,+∞)上恒成立,求实数a的取值范围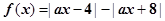 ,
,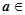 R
R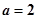 时,解不等式
时,解不等式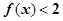 ;
;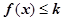 恒成立,求k的取值范围.
恒成立,求k的取值范围.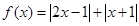 .
.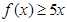 ;
;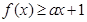 的解集为
的解集为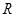 ,求实数
,求实数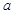 的取值范围.
的取值范围. 的解集为M.
的解集为M.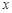 的不等式
的不等式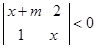 的解集为
的解集为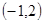 。
。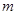 的值;
的值;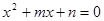 的一个根
的一个根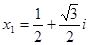 ,求
,求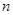 .
. 的不等式
的不等式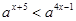 (
(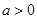 ,且
,且 ).
).