题目内容

若M（x，y）在直线上x+2y+1=0移动，则2x+4y的最小值是（　　）
分析：根据M（x，y）在直线上x+2y+1=0移动，所以x+2y=-1，然后利用基本不等式求2x+4y的最小值．
解答：解：因为M（x，y）在直线上x+2y+1=0移动，所以x+2y=-1．
所以2x+4y≥2
2x•4y
=2
2x+2y
=2
2-1
=
2
．
所以2x+4y的最小值是
2
．
故选B．
点评：本题主要考查基本不等式的应用，注意基本不等式成立的条件．
练习册系列答案
相关题目
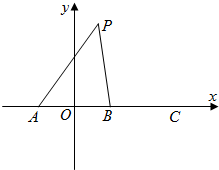精英家教网如图，在直角坐标系中，A，B，C三点在x轴上，原点O和点B分别是线段AB和AC的中点，已知AO=m（m为常数），平面上的点P满足PA+PB=6m．
（1）试求点P的轨迹C1的方程；
（2）若点（x，y）在曲线C1上，求证：点(
x
3
，
y
2
2
)一定在某圆C2上；
（3）过点C作直线l，与圆C2相交于M，N两点，若点N恰好是线段CM的中点，试求直线l的方程．
若M（x，y）在直线上x+2y+1=0移动，则2x+4y的最小值是（　　）
A．
2
2
B．
2
C．2
2
D．4
2
若M（x，y）在直线上x+2y+1=0移动，则2x+4y的最小值是（ ）
A．
B．
C．
D．
已知椭圆C1：=1和圆C：x2+y2=4，且圆C与x轴交于A1，A2两点．
（1）设椭圆C1的右焦点为F，点P的圆C上异于A1，A2的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明；
（2）设点M（x，y）在直线x+y-3=0上，若存在点N∈C，使得∠OMN=60°（O为坐标原点），求x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网