题目内容
函数 (A>0,ω>0)的最大值为2,其最小正周期为π.
(A>0,ω>0)的最大值为2,其最小正周期为π.
(1)求函数f(x)的解析式;
(2)设 ,则
,则 ,求cosα的值.
,求cosα的值.
解:(1)由题意A=2,…(2分)
∵最小正周期T=π,∴ω=2…(4分)
故函数f(x)的解析式为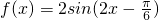 …(5分)
…(5分)
(2)∵ ,即
,即 ,…(6分)
,…(6分)
∵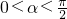 ,∴
,∴ ,…(7分)
,…(7分)
∴ ,
, ,…(10分)
,…(10分)
故 …(12分)
…(12分)
(或)∵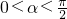 ,∴
,∴ ,
,
∴ ,…(9分)
,…(9分)
故 …(12分)
…(12分)
分析:(1)通过函数的最大值,求出A,函数的最小正周期求出ω,然后求出函数f(x)的解析式;
(2)根据 ,与
,与 ,求出α-
,求出α- 的值,然后求出α的值,即可利用cosα通过两角和与差的余弦函数求出它的值.
的值,然后求出α的值,即可利用cosα通过两角和与差的余弦函数求出它的值.
点评:本题考查三角函数的解析式的求法,两角和与差的三角函数的应用,函数值的求法,考查计算能力.
∵最小正周期T=π,∴ω=2…(4分)
故函数f(x)的解析式为
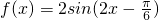 …(5分)
…(5分)(2)∵
 ,即
,即 ,…(6分)
,…(6分)∵
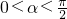 ,∴
,∴ ,…(7分)
,…(7分)∴
 ,
, ,…(10分)
,…(10分)故
 …(12分)
…(12分)(或)∵
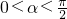 ,∴
,∴ ,
,∴
 ,…(9分)
,…(9分)故
 …(12分)
…(12分)分析:(1)通过函数的最大值,求出A,函数的最小正周期求出ω,然后求出函数f(x)的解析式;
(2)根据
 ,与
,与 ,求出α-
,求出α- 的值,然后求出α的值,即可利用cosα通过两角和与差的余弦函数求出它的值.
的值,然后求出α的值,即可利用cosα通过两角和与差的余弦函数求出它的值.点评:本题考查三角函数的解析式的求法,两角和与差的三角函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
若函数f(x)=sinax+cosax(a>0)的最小正周期为π,则它的图象的一个对称中心为( )
A、(-
| ||
B、(
| ||
| C、(0,0) | ||
D、(-
|
 已知定义在R上的函数f(x)=asinωx+bcosωx(ω>0,a>0,b>0)周期为
已知定义在R上的函数f(x)=asinωx+bcosωx(ω>0,a>0,b>0)周期为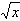 ,g(x)=alnx,a∈R。
,g(x)=alnx,a∈R。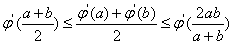 。
。