题目内容
【题目】己知![]() .
.
(1)解关于x的不等式![]() ;
;
(2)若![]() 的解集为R,求a的取值范围.
的解集为R,求a的取值范围.
【答案】(1)当![]() ;当
;当![]() ;当
;当![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 得
得![]() ,即
,即![]() ,对
,对![]() 分三种情况讨论:①当
分三种情况讨论:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别求解不等式;
时,分别求解不等式;
(2)分别得出![]() 分段函数的解析式,做出满足题意的图像,根据数形结合,得出关于
分段函数的解析式,做出满足题意的图像,根据数形结合,得出关于![]() 的不等式,解之可得出a的取值范围.
的不等式,解之可得出a的取值范围.
(1)由![]() 得
得![]() ,所以
,所以![]() 即
即![]() ,
,
①当![]() 时,不等式化为
时,不等式化为![]() ,所以此时不等式的解集为
,所以此时不等式的解集为![]() ;
;
②当![]() 时,不等式化为
时,不等式化为![]() ,所以此时不等式的解集为
,所以此时不等式的解集为![]() ;
;
③当![]() 时,不等式化为
时,不等式化为![]() ,所以此时不等式的解集为
,所以此时不等式的解集为![]() ;
;
综上可得:
①当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
②当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
③当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
(2)当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 恒成立,所以
恒成立,所以![]() 满足
满足![]() 的解集为
的解集为![]() ;
;
而![]() ,
,
当![]() 时,
时,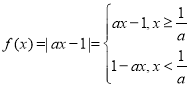 ,
,
当![]() 时,
时,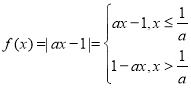 ,做出
,做出![]() 的图像如下图所示,
的图像如下图所示,
要使![]() 的解集为
的解集为![]() ,则需
,则需![]() 或
或![]() ,解得
,解得![]() 或
或![]() ;
;
综上可得:a的取值范围是![]() .
.

练习册系列答案
相关题目