题目内容
若P( ,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,-
,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,-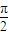 <φ<
<φ< )的图象的一个对称中心,且点P到该图象对称轴的距离的最小值为
)的图象的一个对称中心,且点P到该图象对称轴的距离的最小值为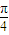 ,则( )
,则( )A.ω=1,φ=
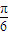
B.ω=1,φ=-
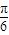
C.ω=2,φ=

D.ω=2,φ=-
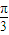
【答案】分析:由题意可得 B=2, =
= ×
× ,解得ω的值,再由Asin(2×
,解得ω的值,再由Asin(2× +∅)=0,且-
+∅)=0,且- <φ<
<φ< ,可得∅的值.
,可得∅的值.
解答:解:∵P( ,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,-
,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,- <φ<
<φ< )的图象的一个对称中心,故 B=2,
)的图象的一个对称中心,故 B=2,
∵点P到该图象对称轴的距离的最小值为 ,则
,则 =
= T=
T= ×
× ,解得ω=2.
,解得ω=2.
再由Asin(2× +∅)=0,且-
+∅)=0,且- <φ<
<φ< ,可得∅=-
,可得∅=- .
.
故选D.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,正弦函数的对称性,属于中档题.
 =
= ×
× ,解得ω的值,再由Asin(2×
,解得ω的值,再由Asin(2× +∅)=0,且-
+∅)=0,且- <φ<
<φ< ,可得∅的值.
,可得∅的值.解答:解:∵P(
 ,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,-
,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,- <φ<
<φ< )的图象的一个对称中心,故 B=2,
)的图象的一个对称中心,故 B=2,∵点P到该图象对称轴的距离的最小值为
 ,则
,则 =
= T=
T= ×
× ,解得ω=2.
,解得ω=2.再由Asin(2×
 +∅)=0,且-
+∅)=0,且- <φ<
<φ< ,可得∅=-
,可得∅=- .
.故选D.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,正弦函数的对称性,属于中档题.

练习册系列答案
相关题目
 ,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,-
,2)是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,- <φ<
<φ< ,则
,则