题目内容
 ( )
( )A. | B. |
C. | D. |
A
分析:利用y=sinx的增区间为[2kπ-  ,2kπ+
,2kπ+  ],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,求出[2kπ-
],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,求出[2kπ-  ,2kπ+
,2kπ+ ]∩[2kπ-π,2kπ]的结果即为所求.
]∩[2kπ-π,2kπ]的结果即为所求.
解答:解:函数y=sinx的增区间为[2kπ- ,2kπ+
,2kπ+ ],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,
],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,
由[2kπ- ,2kπ+
,2kπ+ ]∩[2kπ-π,2kπ]=[2kπ-
]∩[2kπ-π,2kπ]=[2kπ- ,2kπ],
,2kπ],
可得满足函数y=sinx和y=cosx都是增函数的区间是[2kπ- ,2kπ],
,2kπ],
故选A.
点评:本题考查正弦函数、余弦函数的单调增区间,得到正弦函数、余弦函数的单调增区间 是解题的关键.
 ,2kπ+
,2kπ+  ],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,求出[2kπ-
],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,求出[2kπ-  ,2kπ+
,2kπ+ ]∩[2kπ-π,2kπ]的结果即为所求.
]∩[2kπ-π,2kπ]的结果即为所求.解答:解:函数y=sinx的增区间为[2kπ-
 ,2kπ+
,2kπ+ ],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,
],y=cosx的增区间为[2kπ-π,2kπ],k∈Z,由[2kπ-
 ,2kπ+
,2kπ+ ]∩[2kπ-π,2kπ]=[2kπ-
]∩[2kπ-π,2kπ]=[2kπ- ,2kπ],
,2kπ],可得满足函数y=sinx和y=cosx都是增函数的区间是[2kπ-
 ,2kπ],
,2kπ],故选A.
点评:本题考查正弦函数、余弦函数的单调增区间,得到正弦函数、余弦函数的单调增区间 是解题的关键.

练习册系列答案
相关题目
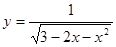 的定义域为( )
的定义域为( )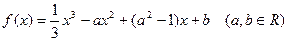 .
.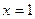 为
为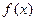 的极值点,求
的极值点,求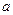 的值;
的值;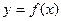 的图象在点(
的图象在点(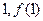 )处的切线方程为
)处的切线方程为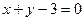 ,
,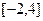 上的最大值;
上的最大值;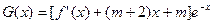 (
(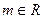 )的单调区间.
)的单调区间. 且
且 则
则 ( )
( )



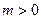 ,
,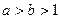 ,
,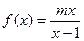 ,比较
,比较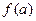 与
与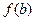 的大小。
的大小。 满足
满足 ,
, 的值为 ;
的值为 ;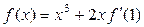 ,则
,则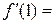 .
.  的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则 ( )
( ) 且
且
 且
且
