题目内容
解不等式:1<|x-2|≤3.
思路分析:已知不等式可化为不等式组来解,也可利用绝对值的意义脱去绝对值求解.
解:方法一:原不等式组就是
![]()
由(1)得x<1或x>3.
由(2)得-1≤x≤5,由下图,
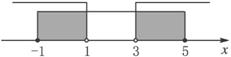
所以原不等式组的解集是{x|-1≤x<1或3<x≤5}.
方法二:原不等式组的解集是下面两个不等式组解集的并集:(1)![]()
或(2)![]()
即1≤x-2≤3或-3≤x-2<-1.
解之得{x|3<x≤5}或{x|-1≤x<1}.
所以原不等式组的解集是{x|-1≤x<1或3<x≤5}.

练习册系列答案
相关题目