题目内容
设函数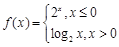 ,若对任意给定的
,若对任意给定的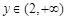 ,都存在唯一的
,都存在唯一的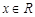 ,满足
,满足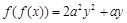 ,则正实数
,则正实数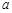 的最小值是( )
的最小值是( )
A.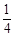 | B.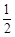 | C.2 | D.4 |
A
解析试卷分析:首先写出f(f(x))表达式,当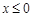 时,
时,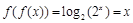 ;当
;当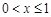 时,
时,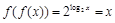 ;当
;当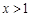 时,
时,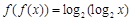 ,考虑到题目说的要求x的唯一性,即当取某个y值时,f(f(x))的值只能落在三段区间的一段,而不能落在其中的两段或者三段内。因此我们要先求出f(f(x))在每段区间的值域。当
,考虑到题目说的要求x的唯一性,即当取某个y值时,f(f(x))的值只能落在三段区间的一段,而不能落在其中的两段或者三段内。因此我们要先求出f(f(x))在每段区间的值域。当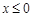 时,
时,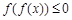 ;当
;当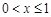 时,
时,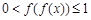 ;当
;当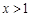 时,
时, 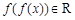 .从中可发现,上面两段区间的值包含在最后一段区间内,换一句话就是说假如f(f(x))取在小于等于1的范围内的任何一个值,则必有两个x与之对应。因此,考虑到x的唯一性,则只有使得f(f(x))>1,因此题目转化为当y>2时,恒有
.从中可发现,上面两段区间的值包含在最后一段区间内,换一句话就是说假如f(f(x))取在小于等于1的范围内的任何一个值,则必有两个x与之对应。因此,考虑到x的唯一性,则只有使得f(f(x))>1,因此题目转化为当y>2时,恒有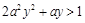 。因此令
。因此令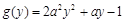 ,题目转化为y>2时,恒有g(y)>0,又g(y)=(2ay-1)(ay+1),为了要使其大于0,则
,题目转化为y>2时,恒有g(y)>0,又g(y)=(2ay-1)(ay+1),为了要使其大于0,则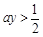 或
或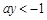 ,考虑到题目要求a的正实数,则ay<-1不考虑。因此
,考虑到题目要求a的正实数,则ay<-1不考虑。因此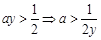 ,在y大于2的情况下恒成立。因此
,在y大于2的情况下恒成立。因此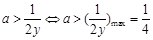 ,所以a的最小正实数为
,所以a的最小正实数为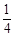 (因为y本身取不到2,因此a可以取
(因为y本身取不到2,因此a可以取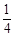 ).
).
考点:1.指数与对数的运算;2.不等式恒成立问题;3.函数的值域.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
函数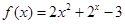 的零点个数为( )
的零点个数为( )
| A.0 | B.1 | C.2 | D.无数 |
若函数 有两个不同的零点,则实数
有两个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设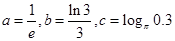 则的大小关系是 ( )
则的大小关系是 ( )
A.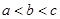 | B.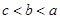 | C.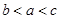 | D.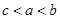 |
若点 在函数
在函数 的图象上,则函数
的图象上,则函数 的值域为( )
的值域为( )
A. | B. |
C. | D. |
已知函数 满足
满足 ,且
,且 是偶函数,当
是偶函数,当 时,
时, ,若在区间
,若在区间 内,函数
内,函数 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )
A. | B. | C. | D. |
函数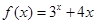 的零点所在的区间是( )
的零点所在的区间是( )
A.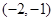 | B.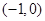 | C.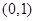 | D.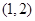 |
已知a>0,且a≠1,loga3<1,则实数a的取值范围是( )
| A.(0,1) | B.(0,1)∪(3,+∞) |
| C.(3,+∞) | D.(1,2)∪(3,+∞) |

