题目内容
已知函数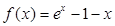
(Ⅰ)求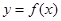 在点
在点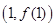 处的切线方程;
处的切线方程;
(Ⅱ)若存在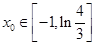 ,满足
,满足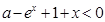 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)当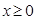 时,
时,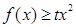 恒成立,求
恒成立,求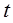 的取值范围.
的取值范围.
(1) (2)
(2)  <
<
(3)
解析试题分析:解:(Ⅰ) 

 在
在 处的切线方程为:
处的切线方程为: 
即 3分
3分
(Ⅱ)  即
即 令
令

 时,
时,  ,
, 时,
时, 
 在
在 上减,在
上减,在 上增
上增
又 时,
时, 的最大值在区间端点处取到.
的最大值在区间端点处取到.



 在
在 上最大值为
上最大值为 ,
,
故 的取值范围是:
的取值范围是: <
< . 8分
. 8分
(Ⅲ)由已知得 时
时 恒成立,设
恒成立,设

由(Ⅱ)知 ,当且仅当
,当且仅当 时等号成立,
时等号成立,
故 从而当
从而当
即 时,
时, ,
, 为增函数,又
为增函数,又
于是当 时,
时, 即
即
 时符合题意。11分
时符合题意。11分
由 可得
可得 ,从而当
,从而当 时,
时,
故当 时,
时, ,
, 为减函数,又
为减函数,又 ,
,
于是当 时,
时, 即
即
故 ,不符合题意.
,不符合题意.
综上可得 的取值范围为
的取值范围为 14分
14分
考点:导数的运用
点评:解决的关键是利用导数的几何意义求解切线方程以及根据导数的符号判定函数单调性,得到函数的最值,属于基础题。

练习册系列答案
相关题目
 上有意义的两个函数
上有意义的两个函数 如果有任意
如果有任意
 则称
则称 与
与 在
在 与
与 给定区间
给定区间 , 讨论
, 讨论 与
与 在给定区间
在给定区间 ,当
,当 时函数
时函数 取得一个极值,其中
取得一个极值,其中 .
. 与
与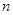 的关系式;
的关系式; 时,函数
时,函数 的图象上任意一点的切线的斜率恒大于
的图象上任意一点的切线的斜率恒大于 ,求
,求 .
. 时,
时, 取得极值,求实数
取得极值,求实数 的值;
的值;
 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数 。
。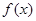 在点
在点 处的切线方程;
处的切线方程; 的最大值与最小值。
的最大值与最小值。 的定义域;(6分)
的定义域;(6分) 在
在 上的值域.(6分)
上的值域.(6分)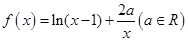
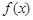 的单调区间;
的单调区间;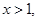 且
且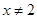 时,
时,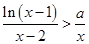 恒成立,求实数
恒成立,求实数 的范围.
的范围.