题目内容
18. 在平面直角坐标系中,O为坐标原点,点A($\sqrt{3}$,1),点B是x轴上一点,AB⊥OA,△OAB的外接圆为圆C.
在平面直角坐标系中,O为坐标原点,点A($\sqrt{3}$,1),点B是x轴上一点,AB⊥OA,△OAB的外接圆为圆C.(1)求圆C的方程;
(2)求圆C在点A处的切线方程.
分析 (1)设B(a,0),
由AB⊥OA,∴$\overrightarrow{OA}•\overrightarrow{AB}$=($\sqrt{3}$,1)•(a-$\sqrt{3}$,-1)=$\sqrt{3}$a-3-1=0,∴$a=\frac{4}{\sqrt{3}}$
即△OAB的外接圆为圆C的圆心为C($\frac{2\sqrt{3}}{3}$,0),半径r=$\frac{2\sqrt{3}}{3}$,即可求解.
(2)由kAC=$\frac{1}{\sqrt{3}-\frac{2\sqrt{3}}{3}}=\sqrt{3}$,得圆C在点A处的切线斜率k=-$\frac{\sqrt{3}}{3}$
即可得圆C在点A处的切线方程.
解答 解:(1)设B(a,0),
∵AB⊥OA,∴$\overrightarrow{OA}•\overrightarrow{AB}$=($\sqrt{3}$,1)•(a-$\sqrt{3}$,-1)=$\sqrt{3}$a-3-1=0,∴$a=\frac{4}{\sqrt{3}}$
∵△ABO是Rt△,∴△OAB的外接圆为圆C的圆心为C($\frac{2\sqrt{3}}{3}$,0),半径r=$\frac{2\sqrt{3}}{3}$
∴圆C的方程为:(x-$\frac{2\sqrt{3}}{3}$)2+y2=$\frac{4}{3}$;
(2)∵kAC=$\frac{1}{\sqrt{3}-\frac{2\sqrt{3}}{3}}=\sqrt{3}$,∴圆C在点A处的切线斜率k=-$\frac{\sqrt{3}}{3}$
∴圆C在点A处的切线方程为y=-$\frac{\sqrt{3}}{3}$x+2.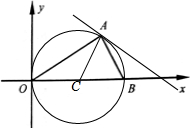
点评 本题考查了圆的方程,圆的切线方程,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 20 |
 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )| A. | 216-20π | B. | 216-26π | C. | 216-60π | D. | 216-54π |
| A. | π | B. | 2π | C. | 4π | D. | 6π |
| A. | 丙团队一定去A景点 | B. | 乙团队一定去C景点 | ||
| C. | 甲团队一定去B景点 | D. | 乙团队一定去A景点 |
| A. | -$\frac{16}{65}$ | B. | $\frac{56}{65}$ | C. | $\frac{16}{65}$或$\frac{56}{65}$ | D. | $\frac{16}{65}$ |