Question

【题目】已知函数.

（Ⅰ）若，求函数在上的零点个数（为自然对数的底数）；

（Ⅱ）若恰有一个零点，求的取值集合；

（Ⅲ）若有两零点，求证：.

Answer 1

【答案】（1）1（2）{1}（3）见解析

【解析】

（Ⅰ）先求出，再结合单调性及函数零点的概念可解得零点的个数；

（Ⅱ）求出并求出极值点，结合单调性，讨论，及时分别对a进行讨论得出的取值集合；

（Ⅲ）先证.根据a建立等式关系，再结合换元法，用t表示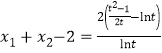，再建立新函数，根据的单调性及最值可证得，再证明，利用，根据可解出（记）.，结合（Ⅰ）可知，建立新函数，再利用导数结合的单调性可得出、的不等式，整理可证的结论.

（Ⅰ）由题设，，故在上单调递减.

所以在上至多只有一个零点.

又，故函数在上只有一个零点.

（Ⅱ），令得.

当时，.在上单调递减；

当时，.在上单调递增.

故.

（1）当，即时，因为最大值点唯一，故符合题设；

（2）当，即时，恒成立，不合题设；

（3）当，即时，一方面，；另一方面，（易证：时，），于是有两个零点，不合题设.

综上，的取值集合为.

（Ⅲ）先证.

依题设，有，于是.

记，则，故.

于是.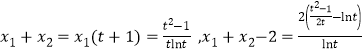

记函数.

因为，故在上单调递增.

于是时，.

又，所以.

再证：.

因为，故，也是的两零点.

由，得（记）.

仿（1）知是的唯一最大值点，故有.

记函数，则，故在上单调递增.

故当时，；当时，.

于是

整理，得，

即.

同理，.

故，

，

于是. 综上，.