题目内容
18.在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,A=2B,求$\frac{a}{b}$的取值范围.分析 A=2B,利用正弦定理可得:$\frac{a}{b}$=$\frac{sinA}{sinB}$=2cosB,由$\frac{π}{2}$<A+B=3B<π,$0<A,B<\frac{π}{2}$,可得$\frac{π}{6}$<B<$\frac{π}{4}$,即可得出.
解答 解:在锐角三角形ABC中,∵A=2B,
∴$\frac{a}{b}$=$\frac{sinA}{sinB}$=$\frac{2sinBcosB}{sinB}$=2cosB,
∵$\frac{π}{2}$<A+B=3B<π,$0<A,B<\frac{π}{2}$,
∴$\frac{π}{6}$<B<$\frac{π}{4}$,
∴$\frac{\sqrt{2}}{2}$<cosB<$\frac{\sqrt{3}}{2}$,
∴$\frac{a}{b}$∈$(\sqrt{2},\sqrt{3})$.
点评 本题考查了正弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知△ABC的三个顶点坐标分别为A(-2,3),B(-2,-1),C(6,-1),以原点为圆心的圆与此三角形有唯一的公共点,则圆的方程为( )
| A. | x2+y2=1 | B. | x2+y2=4 | ||
| C. | x2+y2=$\frac{16}{5}$ | D. | x2+y2=1或x2+y2=37 |
9.现有编号从一到四的四个盒子,甲把一个小球随机放入其中一个盒子,但有$\frac{1}{5}$的概率随手扔掉.然后让乙按编号顺序打开每一个盒子,直到找到小球为止(或根本不在四个盒子里).假设乙打开前两个盒子没有小球,则小球在最后一个盒子里的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
13.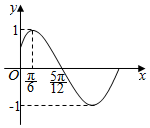 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
12.在某校冬季长跑活动中,学校要给获得一二等奖的学生购买奖品,要求花费总额不得超过200元,已知一等奖和二等奖奖品的单价分别为20元、10元,一等奖人数与二等奖人数的比值不得高于$\frac{1}{3}$,且获得一等奖的人数不能少于2人,那么下列说法中错误的是( )
| A. | 最多可以购买4份一等奖奖品 | B. | 最多可以购买16份二等奖奖品 | ||
| C. | 购买奖品至少要花费100元 | D. | 共有20种不同的购买奖品方案 |